高考第一次教学质量检测数学模拟题(三)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.已知集合M={x![]() },N={y y=3x2+1,xÎR},则MÇN=
},N={y y=3x2+1,xÎR},则MÇN=
A.{xx³1} B.{x x³1或x<0} C.{x x³0或x<1} D.{xx>1}
2.若复数![]() 所对应的点在第四象限,则
所对应的点在第四象限,则![]() 所在的象限是
所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知![]() ,且
,且![]() 与
与![]() 平行,则
平行,则![]() 等于 A.1 B
等于 A.1 B![]() D.
D.![]()
4.![]() = A.1 B
= A.1 B![]() D.
D.![]()
5.在![]() 的展开式中,
的展开式中,![]() 的幂指数是正整数的项共有 A.3项 B.4项 C.5项 D.6项
的幂指数是正整数的项共有 A.3项 B.4项 C.5项 D.6项
6.设集合![]() ,选择I的两个非空子集A和B,要使B中最小的数大于A中
,选择I的两个非空子集A和B,要使B中最小的数大于A中
最大的数,则不同的选择方法共有 A.50种 B.49种 C.48种 D.47种
7.已知![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,![]() 是
是![]() 的必要条件,
的必要条件,![]() 是
是![]() 的必要条件.那么
的必要条件.那么![]() 是
是![]()
成立的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
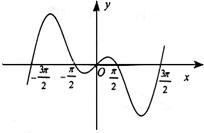 8.函数
8.函数![]() 的部分图象如右图所示,则
的部分图象如右图所示,则![]() 的解析式可以是
的解析式可以是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.已知方程![]() 的四个根组成一个首项为
的四个根组成一个首项为![]() 的等比数列,
的等比数列,
则![]() A.1
B.
A.1
B.![]() C.
C.![]() D.
D.![]()
10.已知函数![]() 满足
满足![]() ,且
,且![]() 在
在![]() 是减函数有以下四个函数:①
是减函数有以下四个函数:①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]()
![]() .其中满足
.其中满足![]() 所有条件的函数序号是
所有条件的函数序号是
A.①② B.② C.②④ D.②③
二、填空题:本大题有4小题,每小题4分,共16分.请将答案填写在题中的横线上.
11.如果![]() ,且
,且![]() 是第一象限的角,则
是第一象限的角,则![]() __________
__________
12.函数![]() 的反函数
的反函数![]() _____________
_____________
13.某大学入学考试各科总分以1000分,2000名应考者的得分分布是平均450分,标准差为75分的正态分布,录取名额为320名,则在录取者中,得分在600分以上的人数约为
人.(其中![]() )
)
14.若![]() ,则下列不等式一定成立的是____(填上所有可能的不等式序号).
,则下列不等式一定成立的是____(填上所有可能的不等式序号).
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
⑤![]()
![]() .
.
三、解答题:本大题有6小题,共84分.解答应写出文字说明,证明过程或演算步骤.
15.已知锐角![]() 中,三个内角为A、B、C,两向量
中,三个内角为A、B、C,两向量![]() ,
,
![]() ,且
,且![]() 与
与![]() 是共线向量.(1)求
是共线向量.(1)求![]() 的大小;
的大小;
(2)求函数![]() 取最大值时,
取最大值时,![]() 的大小。
的大小。
16.一个口袋内装有大小相同且已编有不同号码的4个黑球和3个红球,某人一次从中摸出2个球。(1)如果摸到球中含有红球就中奖,那么此人中奖的概率是多少?(2)如果摸到的两个球都时红球,那么就中大奖,在有放回的3次摸球中,此人恰好两次中大奖的概率是多少?
17.解关于x的不等式:![]() ≤1,其中a>0.
≤1,其中a>0.
18.设![]() ,使
,使![]() ,
,![]() .
.
求证:(1)![]() 且
且![]() ;(2)方程
;(2)方程![]() 在
在![]() 内有两个实根.
内有两个实根.
19.已知函数![]() =
=![]() ,在
,在![]() 处取得极值2.(1)求函数
处取得极值2.(1)求函数![]() 的解析式;
的解析式;
(2)![]() 满足什么条件时,区间
满足什么条件时,区间![]() 为函数
为函数![]() 的单调增区间?(3)若
的单调增区间?(3)若![]() 为
为![]() =
=![]() 图象上的任意一点,直线
图象上的任意一点,直线![]() 与
与![]() =
=![]() 的图象切于
的图象切于![]() 点,求直线
点,求直线![]() 的斜率的取值范围
的斜率的取值范围![]()
20.在数列![]() 中,前
中,前![]() 项和为
项和为![]() .已知
.已知![]() 且
且![]()
(![]() , 且
, 且![]()
![]() ).(Ⅰ)求数列
).(Ⅰ)求数列![]() 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案(3)
DACBA
BACCB ![]()
![]() 40 ②③
40 ②③
15. 解:(1)∵ ![]() ∴
∴ ![]()
∴ ![]() ∴
∴ ![]() ∴
∴ ![]()
∵ ![]() ∴
∴ ![]() ∴
∴ ![]()
(2)∵ ![]() ∴
∴ ![]()
![]()
![]()
∴ 当![]() 时,即
时,即![]() 已知函数
已知函数![]()
(Ⅰ)求函数![]() 的最小正周期; (Ⅱ)求函数
的最小正周期; (Ⅱ)求函数![]() 取得最大值的所有
取得最大值的所有![]() 组成的集合.
组成的集合.
16. (1)记“从袋中摸出的两个球中含有红球”为事件A, 1分
则P(B)=![]() =
=![]() . 5分
. 5分
(或“不含红球即摸出的两个球都是黑球”为事件)![]() .
.
∵P(![]() )=
)=![]() .∴P(A)=-1-P(
.∴P(A)=-1-P(![]() )=
)=![]() . 5分
. 5分
答:此人中奖的概率是![]() . 6分
. 6分
(2)记从“袋中摸出的两个球都是红球”为事件B, 7分
则P(B)=![]() =
=![]() . 10分
. 10分
由于有放回的3次摸,每次是否摸到两个红球之间没有影响.
所以3次摸球恰好有两次中大奖相当于作3次独立重复试验,
根据n次独立重复试验中事件恰好发生k次的概率公式得,
P3(2)=C23(![]() )2·(1-
)2·(1-![]() )3-2=
)3-2=![]() . 13分
. 13分
答:此人恰好两倍欠中大奖的概率是![]() . 14分
. 14分
17. 解:由![]() ,得
,得![]() ,从而
,从而![]() ,于是
,于是![]() .
.
∵![]() ,∴
,∴![]() . ∴原不等式等价于
. ∴原不等式等价于 ![]() ,
,
即![]() , 亦即
, 亦即![]() .
.
∴当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() ;
;
当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() .
.
18.(略)
19. 解:(1)已知函数![]() =
=![]() ,
,![]() (……………2分)
(……………2分)
又函数![]() 在
在![]() 处取得极值2,
处取得极值2,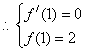 ,即
,即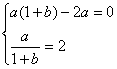
![]()
![]() (……………………5分)
(……………………5分)
由![]()
| x |
|
| (-1,1) | 1 |
|
|
| - | 0 | + | 0 | - |
|
| ↘ | 极小值-2 | ↗ | 极大值2 | ↘ |
所以![]() 的单调增区间为
的单调增区间为![]() ,
(………………8分)
,
(………………8分)
若![]() 为函数
为函数![]() 的单调增区间,则有
的单调增区间,则有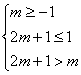
解得![]()
即![]() 时,
时,![]() 为函数
为函数![]() 的单调增区间
的单调增区间![]() (…………………10分)
(…………………10分)
(3)![]()
![]()
![]()
![]()
直线![]() 的斜率为
的斜率为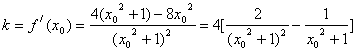 (………12分)
(………12分)
令![]() ,则直线
,则直线![]() 的斜率
的斜率![]() ,
,
![]()
![]() (………………14分)
(………………14分)
20. 19.解:(1).![]() (n
(n![]() N+ , 且n
N+ , 且n![]() )…………①
)…………①
![]() (n
(n![]() N+ , 且n
N+ , 且n![]() )………………………②
)………………………②
①-②得:![]() ………3分
………3分
![]() 又
又![]() ,
∴
,
∴![]()
故: ![]()
![]()
![]()
……… ![]() 上列各式相加得:
上列各式相加得: ![]()
(2).由n![]() =
=![]() 得
得
Tn=![]()
令An=![]()
则2 An=![]() ………9分
………9分
![]() An=
An=![]() ……………10分
……………10分
=![]() =
=![]() ------11分
------11分
![]() Tn=
Tn=![]()
=![]() +
+![]() ----------------------------------14分
----------------------------------14分