高考第一次科目教学质量检测数学模拟题（一）

高考第一次科目教学质量检测数学模拟题（一）

一．选择题：本大题共10小题；每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在数集中，实数x的取值范围是英才苑　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　 D．

2．2＋与2－的等比中项等于　　　　　　　　　　　　　 （　　）

A．1　　　　　　　　　　　　 B．－1　　　　　　　　　 C．2　　　　　　　　　　　　　D．±1

3．化简的结果为　　  （　　 ）

A．0　　　　　　　　　　　　 B．1　　　　　　　　　　　 C．2　　　　　　　　　　　　　D．3

4．在下列极限中，其值等于2的是　　　　　　　　　　　　　  （　　 ）

　A． B．　C．　　D．

5．下列命题：⑴若“p或q”是假命题，则“”是真命题　⑵⑶命题“a,b都是偶数，则a+b是偶数”的逆否命题是“a+b不是偶数，则a,b都不是偶数”其中真命题的是（　 ）

A. ⑴　　  B. ⑵　　　　C. ⑴⑵　　　 D. ⑶

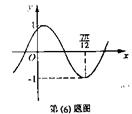6.将函数的图象按向量平移,平移　后的图象如图所示,则平移后的图象所对应的函数解析式是（　　）

Ａ．　　　　　 Ｂ．　　　　

Ｃ．　　　　　Ｄ．　

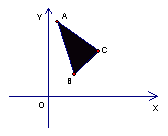
7．已知A(1,6)、B(2,2)、C(4,4)，如图所示的坐标平面的可行域内

(阴影部分包括周界)，若使目标函数取得最大值

的最优解有无穷多个，则a的值等于 (　　)

A．1　　　　　　B．4　　　　　　　C．　　　　　　　　　D．6

8. 已知等差数列的前项和为，若，则下列各式中一定为常数的是（　）

A．　　B．　　C．　　D．

9.已知A、B、C是平面上不共线的三点，O为⊿ABC的外心，动点P满足，则P的轨迹一定通过⊿ABC的 （　）

A.内心　　　　　　B.垂心　　　　　　C.重心　　　　　D.AB边的中点

10．函数，当

（　　）（以下）

　　　 A．　　　　B．　　　　C．　　　 D．

二．填空题（本大题共4分，每题4分，共16分）

11．若复数在复平面上的对应点在第三象限，则实数a的范围为　　　　　　　　　  。

12．已知　　　　  。

　　　 13．已知数列，，把数列的各项　　　　　　　　 a₁

排成三角形状，如图所示．记表示第m行，　　　　　　　　 a₂ a₃

第n列的项，则=　　　　　 。　　　　　　　　　　　　 a₄  a₅ a₆

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……………………

14．地区的一种特色水果上市时间仅能持续5个月，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格连续下跌，现有三种价格模拟函数.① f(x)=p·q;② f(x)=px²+qx+1;③ f(x)=x(x-q)²+p.

　 （以上三式中p、q均为常数，且q＞1，x=0表示4月1日，x=1表示5月1日，依次类推）.

　 （1）为准确研究其价格走势，应选_______种价格模拟函数.

　 （2）若f(0)=4，f(2)=6，预测该果品在_________月份内价格下跌.

三．解答题（本大题共6题，共84分，解答下列各题必须写出必要步骤）

15．（本题满分14分）　已知函数是R上的偶函数，其图象关于点M（，0）对称；

（1）求的值

（2）求的单调递增区间

（3）

16．（本题满分14分）　小张有一只放有a个红球，b个黄球，c个白球的箱子，且a+b+c =6 (a，b，cN)，小刘有一只放有3个红球，2个黄球，1个白球的箱子，两人各自从自己的箱子中任取一球，规定：当两球同色时小张胜，异色时小刘胜.

(1) 用a、b、c表示小张胜的概率；

(2) 若又规定当小张取红、黄、白球而胜的得分分别为1分、2分、3分，否则得0分，求小张得分的期望的最大值及此时a、b、c的值.

17．（本题满分14分）　在数列中，，当n时，其前n项和满足

　 （1）求S_n　　 （2）设,求的前项和

18．(本小题满分14分)　 某公司生产的A型商品通过租赁柜台进入某商场销售．第一年，商场为吸引厂家，决定免收该年管理费，因此，该年A型商品定价为每件70元，年销售量为11.8万件．第二年，商场开始对该商品征收比率为p％的管理费(即销售100元要征收p元)，于是该商品的定价上升为每件元，预计年销售量将减少p万件.

(1) 将第二年商场对该商品征收的管理费y(万元)表示成p的函数，并指出这个函数的定义域；

(2) 要使第二年商场在此项经营中收取的管理费不少于14万元，则商场对该商品征收管理费的比率p％的范围是多少?

(3) 第二年，商场在所收管理费不少于14万元的前提下，要让厂家获得最大销售金额，则p应为多少?　

19．（本题满分14分）　已知在R上单调递增，记△ABC的三内角A，B，C的对应边分别为a，b，c，若时，不等式

恒成立.

　 （I）求实数k的取值范围； （Ⅱ）求角B的取值范围； （Ⅲ）求实数m的取值范围.

20．（本题满分14分）　已知（c为实常数）且，其图象和y轴交于A点；数列为公差为d（d＞0）的等差数列，且a₁=d；点列B_i（a_i，f（a_i­））　　（i=1，2，…，n）

　 （1）求函数的表达式；

　 （2）设p_i为直线AB­_i­的斜率，q_i为直线B_iB_i+1的斜率，求证数列b_n=q_n－p_n仍为等差数列；

　 （3）求 的面积

　　　　　　　　　 数学答题卷　　　　　　 座位号

一.选择题：本大题共10小题，每小题5分，共50分．

题号	1	2	3	4	5	6	7	8	9	10
答案	D	D	D	C	D	C	B	C	D	C

二.填空题：本大题共4小题，每小题4分，共16分．

11.　　（1，2）　　　 12. 　　　2　　　　　13.　　  .14.　3，5月6月

三.解答题：（本大题共6小题，每题14分，共84分．解答题写出必要过程以及演算步骤．）

15.(本小题14分)解:

1）

2）

3）当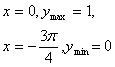

16. (本小题14分)解:

（1）

　　

　　

　　  

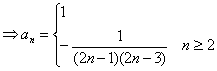
　 （2）　　

17. (本小题14分)解:

(1)P(小张胜)=P(两人均取红球)+P(两人均取黄球)+P(两人均取白球)　

　= + + =　……………………………5分

　(2) 设小张的得分为随机变量，则

　P(=3)= ，P(=2)= ，P(=1)= ，

　P(=0)=1一P(小张胜)=1一，……………………………9分

　∴E=3×+2×+1×+0×(1一)

=

∵ a，b，c∈N，a+b+c=6，∴b =6，此时a=c=0，　　

　∴当b=6时，E最大值为2/3，此时a=c=0，b=6…………………12分

18. (本小题14分)解:

（1）由上单调递增，

，

当

即当k=时，能使f(x)在R上单调递增，

∴k≥.

　 （2），

由余弦定理：

上单调递增，且

所以

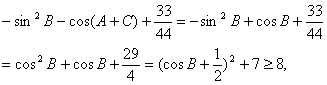
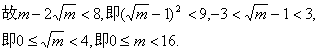
19. (本小题14分)解:

解：(1)依题意，第二年该商品年销售量为(11.8－p)万件，

　年销售收入为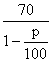 (11.8一户)万元，

 则商场该年对该商品征收的总管理费为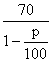 (11·8一p)p％(万元)

 故所求函数为 y=

 由11.8－p>0及p>0得定义域为0<p<11.8　 ……………………………6分

　  (2) 由y≥14得≥14

　化简得p²－12p+20≤0，即(p－2)(p－10)≤0，解得2≤p≤l0

　故当比率为[2％，10％]内时，商场收取的管理费将不少于14万元．…10分

　  (3) 第二年，当商场收取的管理费不少于14万元时，

　厂家的销售收入为g(p)= 　 (2≤p≤10)

　 ∵ g(p)=  =700(10+)为减函数，

　 ∴ g(p)_max =g(2)=700(万元)

故当比率为2％时，厂家销售金额最大，且商场所收管理费又不少于14万元　　　　　　　　　　　　　　　　　　　　　 ………………………14分

20. (本小题14分)解: （1）

∴c=1

　 （2）易得A点为（0，1）

也为等差数列

　 （3）三角形的面积