高考科目教学第一次质量检测数学模拟题（二）
一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，有且只有一项是符合题目要求的.
1.复数z1=3+i，z2=1-i，则z1·z2在复平面内的对应点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知向量
,则向量
与
A.互相平行
B.互相垂直 C.夹角为
D.夹角为
3.对于实数a、b，“b(b－a)≤0”是“
≥1”成立的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
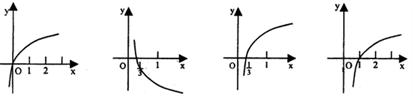4.已知函数
，则它的反函数
的大致图像是
A B C D
5.从8名女生，4名男生中选出6名学生组成课外小组，如果按性别比例分层抽样，则不同的抽取方法种数为 A.C
B.C
C.
D.A
6.设f(x-1)＝x+x2+x3+…+xn，且f(x)中所有项的系数和为
，则
的值为
A.0
B.
C.2
D.1
7.若函数
的图象按向量
平移后，得到的图象关于原点对称，则向量可以是 A.
B.(
，－1) C.
D.
8.设函数f(x)、g(x)在[a,b]上可导，且
，则当
时有 A.
B.
C.
D.
9.一个篮球运动员投篮一次得3分的概率为
，得2分的概率为
，不得分的概率为
（、、
），已知他投篮一次得分的数学期望为
（不计其它得分情况），则
的最大值为 A.
B.
C.
D.
10.设关于x的不等式
和
的解集分别是A、B．下列说法中不正确的是 A.不存在一个常数a使得A、B同时为φ
B.至少存在一个常数a使得A、B都是仅含有一个元素的集合
C.当A、B都是仅含有一个元素的集合时，总有A＝B
D.当A、B都是仅含有一个元素的集合时，总有A≠B
二、填空题：本大题有4小题，每小题4分，共16分.请将答案填写在题中的横线上.
11.函数
的单调递减区间是__________________
12.若
展开式中含
的项是第六项，则
_______
13.已知函数
，则不等式
的解集是__ ___
14.对于函数f(x)=x2(x＞0)图象上任意两点A（a,a2）,B(b,b2),直线段AB必在曲线段AB的上方，设点C分
的比为
，则由图象的特征可得不等式
.请分析y=lgx的图象特征，类比上述不等式可以得到_______________________
三、解答题：本大题有6小题，共84分.解答应写出文字说明，证明过程或演算步骤.
15.已知向量
，记
（1）求
的定义域、值域；（2）若
，其中
，求
.
16.解关于的不等式2＋
.
17.已知函数
在区间
单调递增，在区间
单调递减.
（Ⅰ）求a的值；（Ⅱ）若点A（x0,f(x0)）在函数f(x)的图象上。求证：点A关于直线x=1的对称点B也在函数f(x)的图象上.
18.目前钱塘江上有五座大桥横跨江两岸，据统计各桥梁在一天中流量分别为2、3、4、3、2(单位：万辆),记其中任意三座桥梁在一天中的流量之和为ξ.
（1）求ξ≤8的概率；（2）求随机变量ξ的分布列和数学期望.
19.已知函数
是定义在
上的奇函数,若对于任意
,都有
且＞0时,有＞0.（1）用单调性的定义证明在上为单调递增函数；（2）解不等式
＜
；（3）设
，
若＜
,对所有
,
恒成立,求实数
的取值范围．
20.已知点的序列
，A3是线段A1A2的中点，A4的线段A2A3的中点，…，An是线段An－2An－1的中点，…
（1）写出
、
之间的关系式（n≥3）；
（2）设
，计算
由此推测数列
的通项公式，并用数学归纳法加以证明.
参考答案
1-10 DBBCA CCCBC
11．（1，+∞） 12．11
13．[-1，0）∪（0，3]
14．
15. 答：
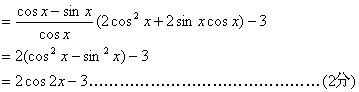
∴定义域为：
…………………（4分）
值域为：
…………………（6分）
（2）
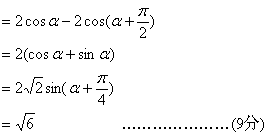
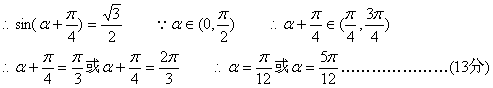
16. 
17.(1)
18．解: (Ⅰ)依题意, ξ的最小值为7, ∵7=2+2+3有两种情况,∴
，
∵8=2+2+4=3+3+1有3种情况,∴
∴
(Ⅱ) )依题意, ξ的可能取值为7,8,9,10
∵9=4＋3+2有
种情况,∴
∵10=4＋3＋3有1种情况,∴
∴ξ的分布列为
| ξ | 7 | 8 | 9 | 10 |
| P |
|
|
|
|
故 Eξ＝
19.（1）证明略
（2） 
（3） 
20.（1）
（2）
