高考数学预测试题(理科)
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P. ![]()
那么n次独立重复试验中恰好发生k次的概 其中R表示球的半径
率![]()
第 I卷 (选择题 共40分)
一.选择题:本大题共8小题,每小题5分,共40分.
1.设集合![]() ≤x≤2},B={x0≤x≤4},则A∩B=
≤x≤2},B={x0≤x≤4},则A∩B=
A.[0,2] B.[1,2] C.[0,4] D.[1,4]
2.已知![]()
A.1+2i B. 1–2i C.2+i D.2–i
3.已知0<a<1,![]() ,则
,则
A.1<n<m B. 1<m<n C.m<n<1 D.n<m<1
4.若![]() 是第二象限的角,且
是第二象限的角,且![]() ,则
,则![]()
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.等差数列![]() 中,
中,![]() ,那么
,那么![]() 的值是
的值是
A. 12 B. 24 C .16 D. 48
6.三棱锥D—ABC的三个侧面分别与底面全等,且AB=AC=![]() ,BC=2,则二面角A—BC—D的大小为
,BC=2,则二面角A—BC—D的大小为
A. 300 B. 450 C.600 D.900
7. 已知变量a,b已被赋值,要交换a、b的值,采用的算法是
A.a=b, b=a B.a=c, b=a, c=b C.a=c, b=a, c=a D.c=a, a=b, b=c
8.已知点M(-3,0),N(3,0),B(1,0),圆C与直线MN切于点B,过M、N与
圆C相切的两直线相交于点P,则P点的轨迹方程为
A.![]() B.
B.![]()
C.![]() (x > 0) D.
(x > 0) D.![]()
第 Ⅱ 卷 (非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分。
9.由数字0、1、2、3、4组成无重复数字的5位数,其中奇数有 个。
10.二项式![]() 的展开式的常数项是__________.
的展开式的常数项是__________.
11.一个正四棱锥的底面边长为2,侧棱长为![]() ,五个顶点都在同一个球面上,则此
,五个顶点都在同一个球面上,则此
球的表面积为 .
12.与直线2x-y-4=0平行且与曲线![]() 相切的直线方程是 .
相切的直线方程是 .
13.圆C: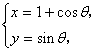 (
(![]() 为参数)的普通方程为__________,设O为坐标原点,
为参数)的普通方程为__________,设O为坐标原点,
点M(![]() )在C上运动,点P(x,y)是线段OM的中点,则点P的轨迹方程为________________。
)在C上运动,点P(x,y)是线段OM的中点,则点P的轨迹方程为________________。
14.设函数![]() ,给出以下四个论断:
,给出以下四个论断:
①![]() 的周期为π; ②
的周期为π; ②![]() 在区间(-
在区间(-![]() ,0)上是增函数;
,0)上是增函数;
③![]() 的图象关于点(
的图象关于点(![]() ,0)对称; ④
,0)对称; ④![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
![]() (只需将命题的序号填在横线上).
(只需将命题的序号填在横线上).
三、解答题(本大题共6小题,共80分)解答应写出文字说明,证明过程或演算步骤。
15.(本小题满分14分)
已知函数![]()
(I)证明:函数![]() 是奇函数;
是奇函数;
(II)求![]() 的单调区间。
的单调区间。
16.(本小题满分12分)
已知 ![]() =1,
=1,![]() =
=![]() ,(I)若
,(I)若![]() //
//![]() ,求
,求![]() ; (II)若
; (II)若![]() ,
,![]() 的夹角为135°,求
的夹角为135°,求 ![]() +
+![]() .
.
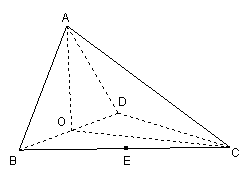 17.(本小题满分14分)
17.(本小题满分14分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
18.(本小题满分14分)
已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支.求:
(Ⅰ)A、B两组中有一组恰有两支弱队的概率;
(Ⅱ)A组中至少有两支弱队的概率.
19.(本小题满分14分)
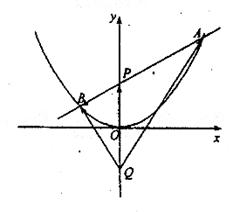
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点。
(Ⅰ)设点P分有向线段![]() 所成的比为λ,证明
所成的比为λ,证明![]()
(Ⅱ)设直线AB的方程是x—2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程。
20.(本小题满分12分)
把正奇数数列![]() 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
— — — —
— — — — —
设![]() 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第![]() 行、从左往右数第
行、从左往右数第![]() 个数。
个数。
(I)若![]() ,求
,求![]() 的值;
的值;
(II)已知函数![]() 的反函数为
的反函数为![]()
![]() ,若记三角形数表中从上往下数第n行各数的和为
,若记三角形数表中从上往下数第n行各数的和为![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() 。
。
高考数学预测试题(理科)答案
班级: 姓名: 座号: 成绩:
一、选择题(每小题5分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | A | C | A | D | B | D | D | B |
二、填空题(每小题5分,共30分)
9. 36 ;10. –540 ;11. 9π ;12.16x-8y+25=0 ;
![]()
![]() 13.
13. ![]() ,
,![]() ;14. ①④
;14. ①④![]() ②③ 或 ①③
②③ 或 ①③![]() ②④ 。
②④ 。
三、解答题(共80分)解答应写出文字说明,证明过程或演算步骤。
15.(本小题满分14分)
解:(I)证明:显然![]() 的定义域是R。设任意
的定义域是R。设任意![]() ,
,
![]() , 4分
, 4分
![]() 函数
函数![]() 是奇函数 6分
是奇函数 6分
(II)解:![]() , 8分
, 8分
令![]() ,由
,由![]() ,解得
,解得![]() 10分
10分
由此可知,当![]() 时,
时,![]() ,
,
所以函数![]() 的单调增区间是(-1,1); 12分
的单调增区间是(-1,1); 12分
当![]() 或
或![]() 时,
时,![]() ,
,
所以函数![]() 的单调减区间分别是(
的单调减区间分别是(![]() ,-1),(1,
,-1),(1,![]() ) 14分
) 14分
(写出的区间,无论是否包含端点均可给分。)
16.(本小题满分12分)
(I)∵![]() //
//![]() ,
,
①若![]() ,
,![]() 共向,则
共向,则 ![]() =
=![]() •
•![]() =
=![]() ………………… 3′
………………… 3′
②若![]() ,
,![]() 异向,则
异向,则 ![]() =-
=-![]() •
•![]() =-
=-![]() ……………… 6′
……………… 6′
(II)∵![]() ,
,![]() 的夹角为135°, ∴
的夹角为135°, ∴ ![]() =
=![]() •
•![]() •cos135°=-1 …… 8′
•cos135°=-1 …… 8′
∴![]() +
+![]() 2=(
2=(![]() +
+![]() )2 =
)2 =![]() 2+
2+![]() 2+2
2+2![]() =1+2-2=1 ………… 11′
=1+2-2=1 ………… 11′
∴![]() ……………………………………12′
……………………………………12′
 17.(本小题满分14分)
17.(本小题满分14分)
方法一:
(I)证明:连结OC
![]()
![]()
 在
在![]() 中,由已知可得
中,由已知可得![]()
而![]()
![]()
![]() 即
即![]()
![]()
![]() 平面
平面![]()
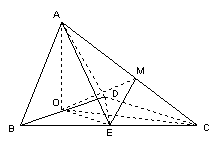
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知![]()
![]() 直线OE与EM所成的锐角就是异面直线AB与CD所成的角
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在![]() 中,
中,
![]()
![]() 是直角
是直角![]() 斜边AC上的中线,
斜边AC上的中线,![]()
![]()
![]() 异面直线AB与CD所成角的大小为
异面直线AB与CD所成角的大小为![]()
(III)解:设点E到平面ACD的距离为![]()
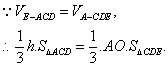
在![]() 中,
中,![]()
![]()
而![]()
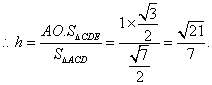
![]() 点E到平面ACD的距离为
点E到平面ACD的距离为![]()
方法二:
(I)同方法一。
(II)解:以O为原点,如图建立空间直角坐标系,则![]()
![]()
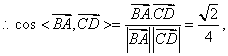
![]() 异面直线AB与CD所成角
异面直线AB与CD所成角
的大小为![]()
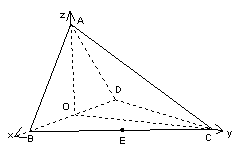 (III)解:设平面ACD的法向量为
(III)解:设平面ACD的法向量为![]() 则
则
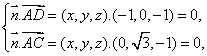
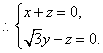
令![]() 得
得![]() 是平面ACD的一个法向量。
是平面ACD的一个法向量。
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离
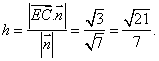
18.(本小题满分14分)
(Ⅰ)解法一:三支弱队在同一组的概率为
![]()
故有一组恰有两支弱队的概率为![]()
解法二:有一组恰有两支弱队的概率![]()
(Ⅱ)解法一:A组中至少有两支弱队的概率 ![]()
解法二:A、B两组有一组至少有两支弱队的概率为1,由于对A组和B组来说,至少有两支弱队的概率是相同的,所以A组中至少有两支弱队的概率为![]()
19.(本小题满分14分)
解(Ⅰ)依题意,可设直线AB的方程为![]() ,代入抛物线方程
,代入抛物线方程![]() 得
得
![]() ①
①
设A、B两点的坐标分别是(x1,y1)、(x2,y2),则x1、x2是方程①的两根。
 所以
所以![]()
由点P(0,m)分有向线段![]() 所成的比为
所成的比为![]() ,
,
得![]() , 即
, 即![]()
又点Q是点P关于原点的以称点,
故点Q的坐标是(0,--m),从而![]()
![]()
=![]()
![]()
=![]()
=![]()
=![]()
=0,
所以![]()
(Ⅱ) 由![]() 得点A、B的坐标分别是(6,9)、(--4,4)。
得点A、B的坐标分别是(6,9)、(--4,4)。
由![]() 得
得![]() ,
, ![]()
所以抛物线![]() 在点A处切线的斜率为
在点A处切线的斜率为![]() 。
。
设圆C的方程是![]() ,
,
则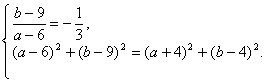
解之得 ![]()
所以圆C的方程是![]() ,
,
20.(本小题满分12分)
解:(I)![]() 三角形数表中前
三角形数表中前![]() 行共有
行共有![]() 个数,
个数,
![]() 第
第![]() 行最后一个数应当是所给奇数列中的第
行最后一个数应当是所给奇数列中的第![]() 项。
项。
故第![]() 行最后一个数是
行最后一个数是![]() 2分
2分
因此,使得![]() 的m是不等式
的m是不等式![]() 的最小正整数解。
的最小正整数解。
由![]() 得
得![]()
![]()
于是,第45行第一个数是![]()
![]() 4分
4分
(II)![]() ,
,![]() 。
。
故![]() 6分
6分
![]() 第n行最后一个数是
第n行最后一个数是![]() ,且有n个数,若将
,且有n个数,若将![]() 看成第n行第一个数,则第n行各数成公差为-2的等差数列,故
看成第n行第一个数,则第n行各数成公差为-2的等差数列,故![]() 。
。
![]() 8分
8分
故![]()
![]() ,
,
两式相减得:
![]() 10分
10分
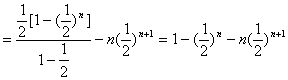
![]() 12分
12分