高三1月月考数学试题(理科)
第I卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1、已知集合![]() ,集合
,集合![]() ,则( )
,则( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、求以抛物线![]() 的焦点为焦点,且离心率为
的焦点为焦点,且离心率为![]() 的椭圆的标准方程为( )
的椭圆的标准方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、已知等差数列![]() 满足:
满足:![]() ,若等比数列
,若等比数列![]() 满足
满足![]() ,则
,则![]() 为( )
为( )
A、16 B、32 C、64 D、27
4、![]() 的图象相邻两对称轴之间的距离为(
)
的图象相邻两对称轴之间的距离为(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、抛物线![]() 在点
在点![]() 处的切线与其平行直线
处的切线与其平行直线![]() 间的距离是( )
间的距离是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、在![]() (O为原点)中,
(O为原点)中,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
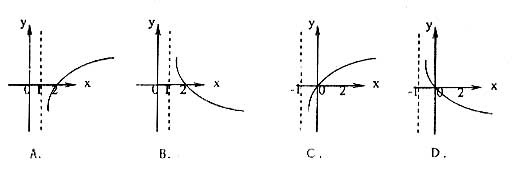
7、若函数![]() (
(![]() 且
且![]() )在
)在![]() 上既是奇函数,又是增函数,则
上既是奇函数,又是增函数,则![]() 的图像是( )
的图像是( )
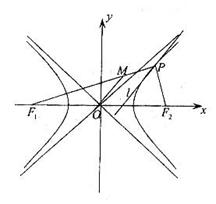
8、设双曲线M:![]() ,过点C
,过点C![]() 且斜率为1的直线,交双曲线的两渐近线于A,B两点,若2
且斜率为1的直线,交双曲线的两渐近线于A,B两点,若2![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、函数![]() 满足:对一切
满足:对一切![]() ,
,![]() ;当
;当![]() 时,
时,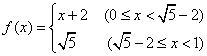 ,则
,则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、正实数![]() 及函数
及函数![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A、4
B、![]() C、2
D、
C、2
D、![]()
第II卷(非选择题 共100分)
二、填空题:本大题共6小题,每小题4分,共24分。把答案填写在答题卡相应位置上。
11、以坐标原点为圆心且与直线![]() 相切的圆方程为
相切的圆方程为
12、若![]() ,则直线
,则直线![]() 的倾斜角为
的倾斜角为
13、已知函数![]() 的反函数为
的反函数为![]() (
(![]() 且
且![]() ),则函数
),则函数![]() 必过定点
必过定点
14、已知 ,则
,则![]() 的最小值为
的最小值为
 15、如右图,它满足
15、如右图,它满足
①第![]() 行首尾两数均为
行首尾两数均为![]()
②表中的递推关系如杨辉三角,
则第![]() 行
行![]() 的第二个数是
的第二个数是
 16、已知双曲线C:
16、已知双曲线C:![]() 为已知常数
为已知常数![]() ,过第一象限内双曲线上任意一点P作切线
,过第一象限内双曲线上任意一点P作切线![]() ,又过原点作
,又过原点作![]() 的平行线交
的平行线交![]() 于M,则
于M,则![]()
三、解答题:本大题共6小题,共76分。解答应写出文字说明、证明过程或演算步骤。
17、(13分)已知向量![]() ,记
,记![]()
(1)求![]() 的周期;
的周期;
(2)若![]() ,其中
,其中![]() ,求
,求![]() 。
。
18、(13分)解不等式![]() (
(![]() 且
且![]() )
)
19、(13分)已知偶函数![]() ,对任意
,对任意![]() ,恒有
,恒有![]() ,
,
求(1)![]() 的值;
的值;
(2)![]() 的表达式
的表达式
(3)令![]() (
(![]() 且
且![]() ),求
),求![]() 在
在![]() 上的最值
上的最值
20、(13分)一列火车从重庆驶往北京,沿途有![]() 个车站(包括起点站重庆和终点站北京)。车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮代各1个,设从第
个车站(包括起点站重庆和终点站北京)。车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮代各1个,设从第![]() 站出发时,邮政车厢内共有邮袋
站出发时,邮政车厢内共有邮袋![]() 个
个![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 为何值时,
为何值时,![]() 的值最大,求出
的值最大,求出![]() 的最大值。
的最大值。
21、(12分)已知椭圆C:![]() ,经过点M
,经过点M![]() ,过点M向
,过点M向![]() 轴作垂线恰经过椭圆C的焦点,(1)求椭圆方程;(2)设直线
轴作垂线恰经过椭圆C的焦点,(1)求椭圆方程;(2)设直线![]() 与椭圆C相交于A,B两点,且满足
与椭圆C相交于A,B两点,且满足![]() 成等差数列。若AB的垂直平分线交
成等差数列。若AB的垂直平分线交![]() 轴于点T,求直线MT的斜率。
轴于点T,求直线MT的斜率。
22、(12分)抛物线![]() 的准线与
的准线与![]() 轴的交点为M,过点M作直线交抛物线于A、B两点
轴的交点为M,过点M作直线交抛物线于A、B两点
(1)求线段AB中点的轨迹方程;
(2)若线段AB的垂直平分线交对称轴于点N![]() ,求证:
,求证:![]() ;
;
(3)若直线![]() 的斜率依次取
的斜率依次取![]() 时,线段AB的垂直平分线与抛物线对称轴的交点依次是
时,线段AB的垂直平分线与抛物线对称轴的交点依次是![]() ,当
,当![]() 时,求
时,求
![]()