高三1月诊断性考试模拟数学试题(文科)
总分150分
第I卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1、函数![]() 的定义域是( )
的定义域是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、设![]() ,若
,若![]() ,则
,则![]() =( )
=( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、双曲线![]() 的渐近线方程为( )
的渐近线方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、等比数列![]() 中,
中,![]() ,则
,则![]() 的值为( )
的值为( )
A、240 B、160 C、40 D、20
5、函数![]() ,则使
,则使![]() 的
的![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、在等差数列![]() 中,
中,![]() ,则
,则![]() =( )
=( )
A、24 B、48 C、78 D、156
7、已知P是直线![]() 与椭圆的交点,
与椭圆的交点,![]() 分别是椭圆的左右焦点,若
分别是椭圆的左右焦点,若![]() ,且
,且![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、已知函数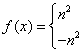
![]() ,且
,且![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 为( )
为( )
A、0 B、10 C、-10 D、100
9、若直线![]() 与椭圆
与椭圆![]() 相交于点P,若
相交于点P,若![]() ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、设定义域为R的函数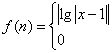
![]() ,若
,若![]() 且
且![]() 时,关于
时,关于![]() 的方程
的方程![]() 的不同实根共有( )个
的不同实根共有( )个
A、4 B、5 C、6 D、7
第II卷(非选择题 共100分)
二、填空题:本大题共6小题,每小题4分,共24分。把答案填空在答题卡上相应位置上。
11、函数![]() 的最小正周期为
的最小正周期为
12、已知向量![]() ,若
,若![]() ,则
,则![]() 的取值范围是
的取值范围是
13、设![]() 满足约束条件
满足约束条件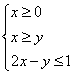 ,则
,则![]() 的最大值是
的最大值是
14、把函数![]() 的图象沿向量
的图象沿向量![]() 的方向平移后,所得图象关于
的方向平移后,所得图象关于![]() 轴对称,则
轴对称,则![]() 的最小值为
的最小值为
15、定义在R上的函数![]() 既是奇数又是周期函数,若
既是奇数又是周期函数,若![]() 的周期为
的周期为![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() =
=
16、已知![]() 与抛物线
与抛物线![]() 相交于A,B两点,则圆C经过A,B且与抛线物在A处的切线相切,则圆C的方程为
相交于A,B两点,则圆C经过A,B且与抛线物在A处的切线相切,则圆C的方程为
三、解答题:本大题共6小题,共76分。解答应写出文字说明、证明过程或演算步骤。
17、(12分)求函数![]() 的最大值及相应的
的最大值及相应的![]() 值。
值。
18、(12分)向量![]() ,向量
,向量![]() ,其中
,其中![]() ,
,![]() 的夹角为
的夹角为![]()
(1) 用![]() 表示
表示![]()
(2) 求![]() 的最大值及此时
的最大值及此时![]() 的值
的值
19、(13分)已知二次函数![]() 满足
满足![]() ,
,![]() 且对任意
且对任意![]() 恒有
恒有![]()
(1) 求![]() 的表达式;
的表达式;
(2) 设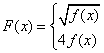
![]() ,解不等式:
,解不等式:![]() 。
。
20、(13分)假设某市2004年新建住房400万平方米,其中有250万平方米是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%,另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米,那么,到哪一年底:
(1)该市历年所建的中低价房的累计面积(以2004年为累计的第一年)将首次不少于4750万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于75%?(其中![]() )
)
21、(13分)设![]() 分别为直角坐标系中
分别为直角坐标系中![]() 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量![]()
![]() 且
且![]() 。
。
(1) 求点M![]() 的轨迹C的方程;
的轨迹C的方程;
(2) 过点![]() 作直线
作直线![]() 与曲线C交于A,B两点,设
与曲线C交于A,B两点,设![]() ,是否存在直线
,是否存在直线![]() 使得四边形OAPB为矩形?若存在,求出直线
使得四边形OAPB为矩形?若存在,求出直线![]() ;若不存在,说明理由。
;若不存在,说明理由。
22、(13分)设![]() 是椭圆
是椭圆![]() 上的一点,且
上的一点,且![]() 构成一个公差为
构成一个公差为![]() 的等差数列,其中O为原点,记
的等差数列,其中O为原点,记![]() 。
。
(1) 若![]() 且
且![]() ,求
,求![]() 的坐标(只需写一个);
的坐标(只需写一个);
(2) 若![]() 且
且![]() ,求
,求![]() 的最大值
的最大值
(3) 点![]() ,对于给定自然数
,对于给定自然数![]() ,当公差
,当公差![]() 变化时,求
变化时,求![]() 的最大值。
的最大值。