专题复习一 函数及其应用
[例题选讲]
[例1] 已知集合![]() ,集合
,集合![]() 满足
满足![]() 求实数
求实数![]() 的值。
的值。
 (答案:
(答案:![]() )
)
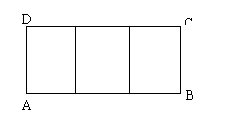
[例2]某工厂计划建造一座底面为矩形ABCD且面积为200
平方米的三级污水处理池(如图所示)。由于受地形限制,
矩形的长与宽都不能超过16米。已知池的外墙建造单价为
每米400元,中间两隔墙建造单价为每米248元,
池底建造单价为每平方米80元。
(1) 试求总造价![]() (元)与矩形长
(元)与矩形长![]() (米)之间的函数关系式
(米)之间的函数关系式![]() ;
;
(2)
|
(答案:(1)![]() ;(2)当x=1时,
;(2)当x=1时,![]() 最小值为45000.)
最小值为45000.)
[例3]已知二次函数![]() 满足
满足![]() 且方程
且方程![]() 有等根。
有等根。
(1)
求![]() 的解析式;
的解析式;
(2)是否存在实数![]() 使
使![]() 的定义域和值域分别为
的定义域和值域分别为![]() 和
和![]() 。如果存在,求出
。如果存在,求出![]() 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
[能力训练]
一、选择题
1.定义![]() ,若
,若![]() ,
,![]() ,则
,则![]() =( )
=( )
(A) A (B)
B
(C) ![]() (D)
(D)
![]()
2.设![]() 在下图中,能表示从集合A到集合B的映射是( )
在下图中,能表示从集合A到集合B的映射是( )
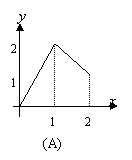
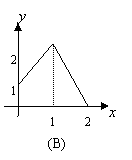
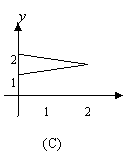
| ||||||||
| ||||||||
|
| |||||||
3.设集合![]() 则下述关系中正确的是( )
则下述关系中正确的是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
4.将函数![]() 的图象先作下面哪一种变化,再作关于直线
的图象先作下面哪一种变化,再作关于直线![]() 对称的图象可得到函数
对称的图象可得到函数![]() 的图象? (
)
的图象? (
)
(A)先向左平行移动1个单位 (B) 先向右平行移动1个单位
(C)先向上平行移动1个单位 (D) 先向下平行移动1个单位
5.下列函数中是偶函数,且又在区间![]() 上是增函数的是( )
上是增函数的是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
6.![]() 在
在![]() 上是单调递增函数,且
上是单调递增函数,且![]() 为奇函数,若
为奇函数,若![]() 的反函数为
的反函数为![]() ,则下列正确的是( )
,则下列正确的是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
7.已知![]() 的定义域是一切实数,则实数
的定义域是一切实数,则实数![]() 的取值范围( )
的取值范围( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
8.定义在R上的偶函数![]() ,满足
,满足![]() ,在区间[-2,0]上单调递减,设
,在区间[-2,0]上单调递减,设![]() ,则
,则![]() 的大小顺序为( )
的大小顺序为( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
 9.在区间
9.在区间![]() 上,函数
上,函数![]() 与
与![]() 在同一点取得相同的最小值,那么
在同一点取得相同的最小值,那么![]() 在
在![]() 上的最大值是( )
上的最大值是( )
(A)![]() (B)4
(C)8
(D)
(B)4
(C)8
(D)![]()
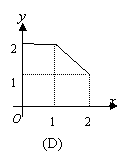
10.如右图所示,四边形ABCD为直角梯形,上底CD为
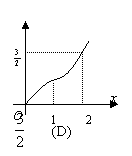 下底AB的一半,直线
下底AB的一半,直线![]() 截这个梯形所得的位于此直线左方
截这个梯形所得的位于此直线左方
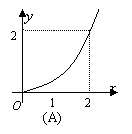
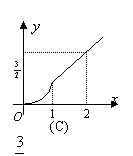
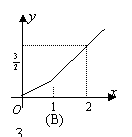
|
11.方程![]() 的两根都大于2,则实数
的两根都大于2,则实数![]() 的范围是( )
的范围是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]() 或
或![]()
12.设函数![]() ,则使
,则使![]() 的
的![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
二、填空题
13.函数![]() 的值域为_______________________。
的值域为_______________________。
14.方程![]() 实数根的个数有__________________。
实数根的个数有__________________。
15.函数![]() ,已知
,已知![]() ,则
,则![]() _________。
_________。
16.我国规定:个人工资、薪金的月总收入不超过800元的免征个人所得税,超过800元部分需征税,全月应纳税的数额(记作![]() )为
)为![]() =全月总收入-800(单位:元)
=全月总收入-800(单位:元)
税率如下表:
| 级数 | 每月应纳税数额 | 税率 |
| 1 |
| 5% |
| 2 | 500< | 10% |
| 3 | 2000< | 15% |
| …… | …… | …… |
| 9 | | 45% |
某人今年5月份工资、薪金总收入是2645元,则此人5月份应交纳的个人所得税额为_______________________。
三、解答题
17.已知![]() ,求函数
,求函数![]() 的最大、最小值。
的最大、最小值。
18.已知![]()
(1)求![]() 的定义域;
的定义域;
(2)讨论![]() 的增减性;
的增减性;
(3)解方程![]() .
.
参考答案:DDCDB AAABC CD
13.![]() 14.2个 15.
14.2个 15.![]() 16、184.50元
16、184.50元
17.![]()
18.(1)a>1时,![]() ;0<a<1时,
;0<a<1时,![]()