专题三平面向量 (1)
一、选择题：
1、下列命题中正确的是 （ ）
A．若a·b = 0，则a = 0或b = 0 B．若 a·b = 0，则a ∥b
C．若a ⊥b，则a·b=（a·b）2 D．若a，b共线，则a·b= a · b
2、化简
＋
－
—
得
（ ）
A．
B．
C．
D．0
3、已知⊿ABC中，A=45°，a=
，b=
，那么满足条件的⊿ABC （ ）
A．有一个 B。有两个 C．不存在 D．不能确定
4.设e1、e2是两个不共线的向量，则向量a=e1+λe2(λ∈R)与向量b=－(e1－2e2)共线的充要条件是
A.λ=0 B.λ=－1
C.λ=2 D.λ=－2
5、已知a ⊥b，a =2， b=3，且3a十2b与λa－b垂直，则λ等于 （ ）
A．
B．
C．
D．1
6、若a ＝3， b=4，（a十b）·（a十3 b）=81，则a与b的夹角是 （ ）
A．30° B．60° C。90° D．120°
7、为了得到函数y= f (－2x)的图象．可以把函数y= f (1－2x)的图象按向量a进行平移，则向量a等于 （ ）
A．（l，0） B．（－l，0） C．（
，0） D．（－，0）
8、已知O为原点，A，B点的坐标分别为（a，0），（0，a），其中常数a＞0，点P在线段AB上．且
＝t（0≤t≤1），则
·
的最大值为
（ ）
A．a B．2a C．3a D．a2
9.与a=(12，5)平行的向量为
A.(
) B.(
)
C.
D.(±
,±
)
10.若点P在线段P1P2的延长线上，P1(4，－3)，P2(－2，6)，且
=4
，则点P的坐标是
A.(9，94) B.(4，9) C.(－4，9) D.(4，－9)
11.若△ABC的周长为7.5 cm，且sinA∶sinB∶sinC=4∶5∶6，则下式成立的个数是
①a∶b∶c=4∶5∶6 ②a∶b∶c=2∶
∶
③a=2 cm,b=2.5 cm,c=3 cm ④A∶B∶C=4∶5∶6
A.0个 B.1个 C.2个 D.3个
12.将函数y=x2进行平移，使得到的图象与抛物线y=－x2+2x+1的两个交点关于原点对称，则平移后函数的解析式是
A.y=x2－2x+3 B.y=x2+4x－3 C.y=x2+2x－1 D.y=x2－2x－3
二、填空题：
13、点（1，3）按向量a平移得到（－1，－1），则点（0，0）按向量a平移得到点的坐标是 。
14、 己知a=(－3，－2)，b=(4，k)，若(5a－b)·(b－3a)=55，则实数k的值为
15.已知a=1，b=2，且(λa+b)⊥(2a－λb),a与b的夹角为60°,则λ=________.
16.已知以下五个命题：
①若a≠0,则a·b=0，则b=0 ②若a=0,则a·b=0
③若a·b=a·c，(其中a、b、c均为非零向量)，则b=c
④若a、b、c均为非零向量，(a·b)·c=a·(b·c)一定成立
⑤已知a、b、c均为非零向量，则a+b+c=a+b+c成立的充要条件是a、b与c同向.
其中正确命题的序号是________.
三、解答题：
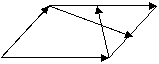17、如图，在平行四边形ABCD中，E，F分别是BC，DC的中点，若=a，=b，试以a，b为基底表示
和
．
D
F
C
E
A B
18、已知平行四边形ABCD的顶点A（
，7），B（2，6），对角钱交点为M（3，），求另外两个顶点C，D的坐标．
19、求与向量a =（，－1）， b =（1，）的夹角相等，且模为的向量C的坐标．
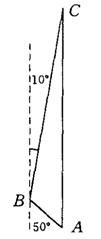20、一缉私艇在岛B南偏东50°相距 8（
）n mile的A处，发现一走私船正由岛B沿方位角为10°方向以 8n mile／h的速度航行，若缉私艇要在2小时时后追上走私船，求其航速和航向．
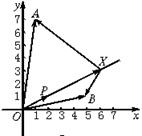
21、如图，已知
=(2,1),
=(1,7),
=(5，1)，
设X是直线上的一点，(其中O为坐标原点).
(1)求使
·
取最小值时的
； (2)对(1)中求出的X，求∠AXB的值.
22.已知△ABC顶点A（0，0），B（4，8），C（6，-4），点M内分所成的比为3，N是AC边上的一点，且△AMN的面积等于△ABC面积的一半，求N点的坐标。
答 案：
自测题
一、1、C 2、D 3、A 4、D 5、A
6、B 7、D 8、D 9、C 10、C 11、C 12、C
10. C 分析：∵λ=－4,
∴x=
=－4,
y=
=9,
∴P(－4,9).
11.C 分析：由正弦定理可得：a=2RsinA,b=2RsinB,c=2RsinC
∴a∶b∶c=sinA∶sinB∶sinC=4∶5∶6,故①、③成立.
12.C 分析：设平移向量为a=(h,k),则y=x2按a平移后为y=(x－k)2+h,设A(x1,y1)与B(－x1,－y1)是y=－x2+2x+1与y=(x－k)2+h的两个交点，可求得x1=－1,y1=－2或x1=1,y1=2.解得h=－1,k=－2，故所求的解析式是y=x2+2x－1.
二、填空题：
13、（－2，－4） 14、－10或－6
15.－1± 分析：∵(λa+b)⊥(2a－λb)
∴(λa+b)·(2a－λb)=0
∴2λa2－λ2a·b+2a·b－λb2=0
∴λ2+2λ－2=0,
∴λ=－1±
16.②、⑤ 分析：(1)a·b=abcosθ=0,
∵a≠0,∴bcosθ=0
∴b=0或cosθ=0
②正确
③a·b=abcosθ,
a·c=accosβ,
由a·b=a·c，可得bcosθ=ccosβ,并不能推出b=c.
④(a·b)与(b·c)都是实数，a与c不一定共线.
⑤正确
三、解答题:
17、解：∵四边形ABCD是平行四边形，E是BC的中点，∴==2
，
∴==b，
==
=－=－a，
∴=++=－++= －b+a+b=a－b，
=+=+=－a + b 。
18、解：（利用对称点有关知识）设C（x1，y1），D (x2，y2)，则M是AC和BD的中点，
即A、C关于M对称．B、D关于M对称，∴ 3=
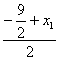x1=
y1=10
又． 3=
x2=4
y2=－3 ∴C，D两点的坐标为C（，10），D（4，－3）。
19、解：设c=(x，y )，则a·c=(,－1)·(x，y )= x－y ，b·c=（1，）·(x，y )= x+y ，设c与a、b的夹角分别为α，β，则
,
由已知得 x2+y2=2
x－y= x+y 解得
，
故C的坐标为（
， 
）
（说明：处理向量a与b的夹角θ，一般有两种途径．一是利用向量的数量积求a与b的夹角θ，二是利用向量的数量积坐标运算求a与b的夹角θ，必须注意θ的范围是0°≤θ≤180°）
20、解：设缉私艇在C处追上走私船．由题意知，在⊿ABC中，AB=8（），BC=16， ∠ABC=120°，则 AC2= AB2＋BC2—2AB·BC·cosABC=[8（）]2+（16）2－2·8（）·16·（—）=82×12。∴AC=16，由正弦定理，得sinA=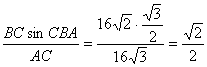
，∴A=45°。即缉私艇应以8 n mile/ h的速度按方 位角 355°方向航行。
21.解：(1)X是直线OP上的点，
∴向量与共线，
∴=t
∴=t(2,1)=(2t,t)
则有：
=(1,7)－(2t,t)=(1－2t,7－t)
=(5,1)－(2t,t)=(5－2t,1－t)
∴·=(1－2t)(5－2t)+(7－t)(1－t)=5(t－2)2－8
当t=2时，·有最小值－8
此时=(2t,t)=(4,2)
(2)当t=2时，=(－3，5)，=(1，－1)
∴=
，=
，且·=－8
∴cosAXB=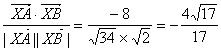
∵0≤∠AXB≤π,
∴∠AXB=π－arccos
.
22.[解] 如图10，
=
=
。
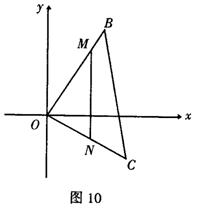
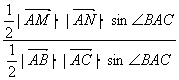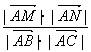∵M分的比为3，∴
=
，则由题设条件得
=
，∴ =
，∴=2。
由定比分点公式得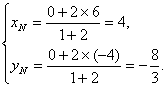
∴N(4,-
)。