专题三平面向量（2）
一、选择题：
1.若
，
，则
的数量积为 （ ）
A．10
B．－10 C．10
D．10
2.若点P分
所成的比为
，则A分
所成的比是（ ）
A.
B.
C.-
D.-
3．若将向量
围绕原点按逆时针方向旋转
得到向量
，则向量的坐标为（ ）
A．
B．
C．
D．
4．在矩形ABCD中，
，当
时，
的值为 ( )
A． B． C．2 D．3
5．已知A（5，7），B（2，3），将
=（4，1）平移后的坐标为 （ ）
A．（－3，－4） B．（－4，－3） C．（1，－3） D．（－3，1）
6．将函数
图象上的点P（1，0）平移至P′（2，0），则经过这种平移后得到的新
函数的解析式为 （ ）
A．
B．
C．
D．
7.设点P分有向线段
的比是λ，且点P在有向线段的延长线上，则λ的取值范围是（ ）
A.(-∞,-1) B.(-1,0) C.(-∞,0) D.(-∞,-
)
8．已知
，则△ABC一定是 （ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰直角三角形
9．若非零向量
互相垂直，则下列各式中一定成立的是 （ ）
A．
B．
C．
D．
10.设四边形ABCD中，有
=，且
=
，则这个四边形是（ ）
A.平行四边形 B.矩形 C.等腰梯形 D.菱形
11.已知平行四边形的3个顶点为A(a,b),B(-b,a),C(0,0)，则它的第4个顶点D的坐标是
A.(2a,b) B.(a-b,a+b) C.(a+b,b-a) D.(a-b,b-a)
12．将椭圆
按向量
平移，使中心与原点重合，则
的坐标为 （ ） A．（2，1） B．（－1，－2） C．（－1，2） D．（1，－2）
二、填空题：
13.在菱形ABCD中，（+）·（-）=
。
14．已知
为单位向量，
=4，
的夹角为
，则
方向上的投影为
.
15．已知
的夹角为120°，且
，
，当
时，
k= .
16．已知点A（－2，－3），B（－1，－6），C（19，4），则△ABC的形状是 .
三、解答题：
17．已知△ABC的顶点坐标为A（1，2），B（2，3），C（3，1），把△ABC按向量
平移后得到
，若的重心为G′（3，4）
求△ABC的对应点A′、B′、C′以及
的坐标.
18．平面内有向量
，
，点M为直线OP上一个动点.
（1）当
取最小值，求
的坐标；
（2）当点M满足（1）的条件和结论时，求
的值.
19.已知a=（cosα，sinα）,b=（cosβ,sinβ），a与b之间有关系ka+b=a－kb， (k>0)
（1）用k表示a·b;
（2）求a·b的最小值，并求此时a·b的夹角的大小。
20.（1）已知a,b是两个非零向量，且a+3b与7a－5b垂直，a－4b与7a－2b垂直，试求a 与b的夹角；
（2）已知：a=,b=3,a和b的夹角为45°，求使向量a+λb与λa+b的夹角是锐角时λ的取值范围。
21.设、
是两个不共线的非零向量（
）
（1）记
那么当实数t为何值时，A、B、C三点共线？
（2）若
，那么实数x为何值时
的值最小？
22.设x , y ∈R，
、
为直角坐标系内x、y轴正方向上的单位向量，若
=x+（y+2），
=x+（y－2），且2+2=16.
（1）求点M（x, y ）的轨迹C 的方程；
（2）过定点（0，3）作直线l与曲线C交于A、B两点，设
，是否存在直线l使四边形OAPB为正方形？若存在，求出l的方程，若不存在说明理由.
答 案
一、选择题：
1．A 2. C 3.B 4.A 5.A 6.A 7. A 8. B 9. B 10. C 11. C 12.B
二、填空题：
13. 0 14．－2 15．
16．直角三角形
三、解答题：
17． 
， A′=（2，4） ， B′=（3，5） ， C′=（4，3）．
18．（1）设M（x,y），当y=2时，
取最小值－8，此时
．
（2）
．
19. 解 （1）要求用k表示a·b,而已知ka+b=a－kb，故采用两边平方，得
ka+b2=(a－kb)2
k2a2+b2+2ka·b=3(a2+k2b2－2ka·b)
∴8k·a·b=(3－k2)a2+(3k2－1)b2
a·b =
∵a=(cosα，sinα),b=(cosβ,sinβ)，
∴a2=1, b2=1,
∴a·b =
=
（2）∵k2+1≥2k，即≥
=
∴a·b的最小值为，
又∵a·b =
a·b ·cos
，a=b=1
∴=1×1×cos。
∴=60°,此时a与b的夹角为60°。
20. 解 （1）∵a+3b与7a－5b垂直，∴（a+3b）·(7a－5b)=0,
即7a2+16a·b－15b2=0， ①
又∵a－4b与7a－2b垂直，∴（a－4b）·(7a－2b)=0。
即7a2－30a·b+8b2=0。 ②
①－②得46a·b=23b2,得a·b=b2,
代入①可得a=b，设所求a与b的夹角为θ，则
cosθ=
=
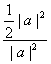=,∴θ=60°。
（2）由已知
a·b=a·b·cos45°=3·
=3。
∵a+λb与λa+b夹角为锐角，
∴（a+λb）·(λa+b)>0，即a·bλ2+(a2+b2) λ+a·b>0。
把a·b=3，a2+b2=a2+b2=2+9=11代入得3λ2+11λ+3>0，
解之得λ<
或λ>
，此即所求λ的取值范围。
注 与代数运算相同，有时可以在含有向量的式子左右两边平方，且有a+b2=(a+b)2=a2+b2+2a·b或a2+b2+2a·b
21. 解：（1）A、B、C三点共线知存在实数
即
，…………………………………………………4分
则
………………………………………………………………6分
（2）
……………………………9分
当
…………………………………………12分
22. 解：（1）由2+2=16得x2+y2=4…………………………4分
（2）假设直线l存在，显然l的斜率存在
设A（x1,y1） B(x2, y2)
由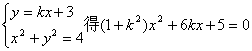
………………6分
∴若OAPB为正方形 只有
即x1x2+y1y2=0
y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9……………………8分
……10分
|
x+3…………………………12分