高三一轮复习检测(集合、函数与导数之二)
1.函数![]() ,已知
,已知![]() 在
在![]() 时取得极值,则
时取得极值,则![]() =( )
=( )
(A)2 (B)3 (C)4 (D)5
2.设![]() ,函数
,函数![]() ,则使
,则使![]() 的
的![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.设函数![]() 为奇函数,
为奇函数,![]() 则
则![]() ( )
( )
A.0 B.1 C.![]() D.5
D.5![]()
4.函数![]() 在区间[1,2]上存在反函数的充分必要条件是( )
在区间[1,2]上存在反函数的充分必要条件是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
![]()
5.函数![]() 上的最大值和最小值之和为a,则a的值为(
)
上的最大值和最小值之和为a,则a的值为(
)
A.![]() B.
B.![]() C.2 D.4
C.2 D.4![]()
6.设集合![]() ,则满足
,则满足![]() 的集合
的集合![]() 的个数是 ( )
的个数是 ( )
A.1 B.3 C.4 D.8
7.若A、B、C为三个集合,![]() ,则一定有
( )
,则一定有
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.若函数![]() 、三、四象限,则一定有( )
、三、四象限,则一定有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
 9.函数
9.函数![]() 的反函数图像大致是
( )
的反函数图像大致是
( )
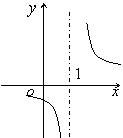
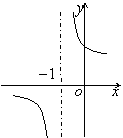
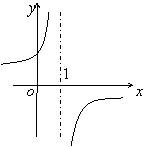 (A)
(B)
(C) (D)
(A)
(B)
(C) (D)
10.函数![]() 有极值的充要条件是
有极值的充要条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.下列关系中正确的是
A.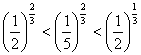 B.
B.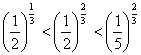
C.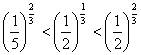 D.
D.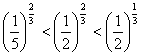
12.若函数![]() 在区间
在区间![]() 内单调递增,则a的取值范围是 ( )
内单调递增,则a的取值范围是 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
13.函数![]() 的定义域为
的定义域为
14.对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)·f(x2);② f(x1·x2)=f(x1)+f(x2)③![]() >0;
>0;
 ④
④![]() .当f(x)=lgx时,上述结论中正确结论的序号是
.当f(x)=lgx时,上述结论中正确结论的序号是
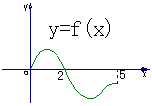
15.设奇函数![]() 的定义域为[-5,5].若当x∈[0,5]时,
的定义域为[-5,5].若当x∈[0,5]时, ![]() 的图象如图,则不等式
的图象如图,则不等式![]() <0的解是
<0的解是
16.设A、B为两个集合,下列四个命题:
①A ![]() B
B![]() 对任意
对任意![]()
②A![]() B
B![]()
![]()
![]()
③A ![]() B
B![]() A
A![]() B
B
④A ![]() B
B![]() 存在
存在![]()
![]()
其中真命题的序号是 (把符合要求的命题序号都填上)
17.设![]() ,函数
,函数![]() 若
若![]() 的解集为A,
的解集为A,![]() ,
,![]() 。求实数
。求实数![]() 的取值范围。
的取值范围。
18.已知![]() (14分)
(14分)
(1)求![]() 的定义域; (2)判断函数的奇偶性 ⑶求使
的定义域; (2)判断函数的奇偶性 ⑶求使![]() 的
的![]() 的取值范围。
的取值范围。
19.已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数。
上是增函数。
(1)如果函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,求
上是增函数,求![]() 的值。
的值。
(2)设常数![]() ,求函数
,求函数![]() 的最大值和最小值;
的最大值和最小值;
;
20.已知两个函数![]() ,
,![]() .
.
(Ⅰ)若对任意![]() [-3,3],都有
[-3,3],都有![]() ≤
≤![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若对任意![]() [-3,3],
[-3,3],![]() [-3,3],都有
[-3,3],都有![]() ≤
≤![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。