高三数学新课标探究题选

高三数学新课标探究题选

1．已知正方体ABCD－A₁B₁C₁D₁的棱长为1，P Î BC₁，Q Î BC，则D₁P + PQ的最小值是C
(A) 2　　　　　　　　　　　　　　　(B) 　　　　　　　　　　　 (C) + 1　　　　  　　 (D)

2．已知函数,给出以下三个条件:

(1) 存在，使得；

(2) 成立；

(3) 在区间上是增函数.

若同时满足条件　　 和　　 （填入两个条件的编号），则的一个可能的解析式为　　　 .

答案：满足条件(1)(2)时,等；满足条件(1)(3)时,等；满足条件(2)(3)时,等.

3．函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等，请选择适当的探究顺序，研究函数f(x)= +的性质，并在此基础上，作出其在的草图．

解：① ∵∴的定义域为R；

② ∵，

 ∴为偶函数；

③ ∵,　∴是周期为的周期函数；

④ 当时，= ，

∴当时单调递减；当时，

=，

单调递增；又∵是周期为的偶函数，∴在上单调递增，在上单调递减（）；

⑤ ∵当时；

当时．∴的值域为；

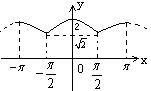
 ⑥由以上性质可得：在上的图象如图所示：

4．有对称中心的曲线叫做有心曲线,显然圆、椭圆、双曲线都是有心曲线. 过有心曲线的中心的弦叫有心曲线的直径,（为研究方便,不妨设直径所在直线的斜率存在）.

　　　 定理：过圆上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值－1.

（Ⅰ）写出该定理在椭圆中的推广,并加以证明；

　　　 （Ⅱ）写出该定理在双曲线中的推广；你能从上述结论得到有心圆锥曲线（包括椭圆、双曲线、圆）的一般性结论吗？请写出你的结论.

解：（Ⅰ）设直径的两个端点分别为A、B,由椭圆的对称性可得,A、B关于中心O（0,0）对称,所以A、B点的坐标分别为A（,B（.

P（上椭圆上任意一点,显然,

因为A、B、P三点都在椭圆上,所以有

, ①

,　②.

而,

由①－②得：

.

所以该定理在椭圆中的推广为：过椭圆上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值.

（Ⅱ）该定理在双曲线中的推广为：过双曲线上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值

　　　 该定理在有心圆锥曲线中的推广应为：过有心圆锥曲线上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值－.

5．已知以坐标原点为中心的椭圆，满足条件

（1）焦点F₁的坐标为 ( 3, 0 )；

（2）长半轴长为5.

则可求得此椭圆方程为 　　　　　（※）

问可用其他什么条件代替条件（2），使所求得的椭圆方程仍为（※）？请写出两种替代条件，并说明理由。

① 短半轴长为4；

② 离心率 e = ；

③ 右准线方程为 x = ；

④ 点P ( 3, ) 在椭圆上；

⑤ 椭圆上两点间的最大距离为10；

　　　　……

　　（答案是开放的，还可写出多种替换条件.）