高三第一次综合练习数学试题
2007．8
一、选择题：
1. 设全集
，集合
={－1，1，2}，
={－1，1}， 
( )
A．{1，2} B．{1} C．{2} D．{－1，1}
2. 已知条件
，条件
，则
是
的
（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
3．下列说法中正确的是 （ ）
A．一个命题的逆命题为真，则它的逆否命题一定为真
B．“
”与“ 
”不等价
C．“
,则
全为
”的逆否命题是“若全不为, 则
”
D．一个命题的否命题为真，则它的逆命题一定为真
4.设
是方程
的解，则属于区间
( )
A.（0，1） B.（1，2） C.（2，3） D.（3，4）
5．设
,则使函数
的定义域为R且为奇函数的所有
的值
为 ( )
A. 1,3 B.-1,1 C. -1,3 D.-1,1,3
6．设
，且
，
，
，则
的大小关系为
（
）
A．
B．
C．
D．
7．函数
的图象大致是 （ ）
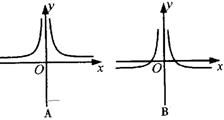
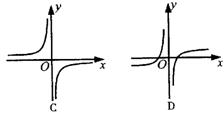
8．如果函数
在区间
上是增函数，那么a的取值范围是（ ）
A．
B．
C．
D．
9. 对于函数
，令集合
，则集合M为 （ ）
A．空集 B．实数集 C．单元素集 D．二元素集
10、在计算机的算法语言中有一种函数
叫做取整函数（也称高斯函数）， 是不超过
的最大整数．例如：
．设函数
,则函数
的值域为
（
）
A.
B.
C.
D. 
二、填空题：
11．log2.56.25＋lg
＋ln
＋
=
12．若函数
的定义域是[1，4]，则函数
的定义域是____________
13．函数
的单调递减区间是_______________
14．函数
的图象F按向量
平移到G，若图象G与函数图象M关于直线
对称，则M的函数解析式为
15．某公司一年需购买某种货物
吨，每次都购买吨，运费为万元/次，一年的总存储费用为
万元，要使一年的总运费与总存储费用之和最小，则
吨.
16．已知函数
时，
只有一个实根；当k∈（0，4）时，只有3个相异实根，现给出下列4个命题：
①
有一个相同的实根；
②
有一个相同的实根；
③
的任一实根；
④
的任一实根.
其中正确命题的序号是
高三数学答题纸
一、选择题：
二、填空题：
11．__________ 12．___________ 13.
14．___________ 15.____________ 16．____________
三、解答题：
17． 设集合
集合C中有三个元素，且满足C∩B≠
，且
，求集合C。
18. 设函数
（1）若
且对任意实数均有
成立，求
表达式；
（2）在（1）在条件下，当
是单调函数，求实数k的取值范围
19．在经济学中，函数的边际函数
定义为
。某公司每月最多生产100台报警系统装置，生产台（
）的收入函数为
（单位：元），其成本函数为
（单位：元），利润是收入与成本之差。
（1） 求利润函数
及边际利润函数
；
（2） 利润函数与边际利润函数是否具有相同的最大值？
20．已知定义在R上的函数满足
为常数
（1）求函数的表达式； （2）如果为偶函数，求的值；
（3）当为偶函数时，若方程
有两个实数根
；其中
，
；求实数
的范围。
21．已知函数
是定义在R上的偶函数, 当
时, =
.
(Ⅰ)求
时, 的解析式;
(Ⅱ)试确定函数y= ()单调区间, 并证明你的结论;
(Ⅲ)若
, 证明:
22．已知函数
，若对任意
，
且
，都有
．
（Ⅰ）求实数的取值范围；
（Ⅱ）对于给定的实数，有一个最小的负数
，使得
时，
都成立，则当为何值时，最小，并求出的最小值．
高三第一次综合练习数学试题答题纸 2007．8
二、填空题（本大题共6小题，每小题5分，共30分。请把答案填在答题纸相应的横线上）
11．_________________ 12．_________________ 13．_________________
14．_________________ 15．_________________ 16．_________________
三、解答题（本大题共6小题，共80分，解答应写出文字说明、证明过程或推演步骤.）
17．
18．
19．
 |
20．
 | |
 |
21．
22．
