高三一轮复习检测（集合、函数与导数之三）
1.集合M=
，则 （ ）
A．M =N B． M 
N C．M
N D．
N
2.已知集合M＝｛x
｝，N＝｛yy＝3x2＋1，xÎR｝，则MÇN＝（ ）
A．Æ B. {xx³1} C.｛xx>1｝ D. {x x³1或x<0}
3.设A、B、I均为非空集合，且满足AB I，则下列各式中错误的是（ ）
A．(
A)∪B=I B．(A)∪(B)=I C．A∩(B)=
D。(A)
(B)= B
4．如果命题“
（
或
）”为假命题，则
（ ）
（A），均为真命题
（B），均为假命题
（C），中至少有一个为真命题
（D），中至多有一个为真命题
5.对于R上可导的任意函数f（x），若满足（x－1）
³0，则必有（ ）
A． f（0）＋f（2）<2f（1） B. f（0）＋f（2）£2f（1）
C. f（0）＋f（2）³2f（1） D. f（0）＋f（2）>2f（1）
|
的图象如右图，若
则（ A ）
A．
B．
C．
D．以上都不正确
7.若loga2＜logb2＜0，则正确的大小关系是（ ）
A．0＜a＜b＜1 B．0＜b＜a＜1 C．a＞b＞1 D．b＞a＞1
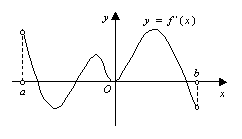8．函数
的定义域为开区间
，导函数
在内的图象如图所示，则函数在开区间内有极小值点（ ）
A．1个 B．2个 C．3个 D． 4个
9．函数y=lg(
)的图象关于
（ ）
A． x轴对称 B．y轴对称 C．原点对称 D．直线y= x对称
10.若与
都是奇函数，且
在
上有最大值
，则在
上
有
A.最小值
B.最大值 C.最小值
D.最小值
11．设函数
的反函数为
，且
的图像过点
，则的图像必过
A． B．
C．
D．
12.设
是方程
的解，则属于区间（ ）
A. （0，1） B. （1，2） C. （2，3） D.（3，4）
13．命题p：“存在实数x，使x2+4x+3＞0”，则“非p”命题是
14．若
，且
，则 a的值为
15、函数
在
上递减，在
上递增，则实数
＝ .
16．函数f(x)=xlnx(x>0)的单调递增区间是
17． 集合A＝｛x｜x2－ax＋a2－19＝0｝，B＝｛x｜x2－5x＋6＝0｝，C＝｛x｜x2＋2x－8＝0｝．
（1）若A∩B＝A∪B，求a的值；
（2）若
A∩B，A∩C＝，求a的值．
18．设函数f(x)= 
x2＋bx＋1（，b∈R）
（1）若f(－1)=0，则对任意实数均有f(x)≥0成立，求f(x)的表达式；
（2）在（1）的条件下，当x∈[－2，2]时，g(x)= f(x)－kx是单调函数，求实数k的取值范围。
19、设是定义在上的增函数，满足
，且
.
（1）求
；
（2）若
，求
的取值范围.
20．已知函数
。 （1）求的值域；（2）若
，求的值域
；（3）在（2）的条件下，若对于任意的
，总存在
使得
，求的取值范围。