高三一轮复习检测（集合、函数与导数之四）
1．已知定义在R上的奇函数f(x)满足f(x+2)=－f(x),则,f(6)的值为 ( )
(A)－1 (B) 0 (C) 1 (D)2
2．若集合
，则A∩B等于( B
)
（A）
. （B）
. （C）
.
（D）
.
3．“a=1”是“函数
在区间[1, +∞)上为增函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4．若
的反函数图象必过定点
，则点的坐标为
A.
B.
C.
D.
5．已知函数f(x)=2x－1，a＜b＜c且f(a)＞f(c)＞f(b)，则 （ ）
A．
＜0，b＜0，c＜0 B. ＜0，b≥0，c＞0 C．2－a＜2c D．2a＋2c＜2
6．已知函数
(
),若
，
则
A.
B.
C.
D.
与
的大小不能确定
7．设
是R上的任意函数,则下列叙述正确的是
A．
是奇函数 B．
是奇函数
C．
是偶函数 D．
是偶函数
8．函数
 |
A． B． C． D
9． 
反函数是（ ）
（A）
（B）
（C）
（D）
10．函数
的单调递增区间为（ ）
（A）（0，
） （B）（
） （C）（
） （D）（
）
11．已知：是R上的增函数，点A（1，3），B（－1，1）在它的图象上，
为它的反函数，则不等式
的解集是（ ）
A．（1，3） B．（2，8） C．（－1，1） D．（2，9）
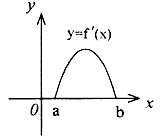
12．
是的导函数，的图象如图所示，则的图象只可能是（ ）
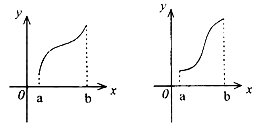
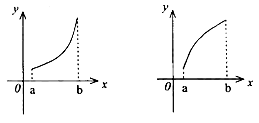
A B C D
13．已知
，奇函数
在
上单调．则字母
应满足的条件是
14．方程x2－2ax＋a＋
=0，有二实根α、β，则（α－1）2＋（β－1）2的最小值为
。
15．已知
函数y=g(x)的图象与y= f－1(x+1)的图象关于y=x对称，则g(11)的值为____________。
16．设函数 
，给出四个命题：① 
=0时，
是奇函数 ；② 
=0，＞0时，方程
只有一个实数根；③ 的图象关于（0，）对称；④ 方程至多有两个实数根；上述命题中正确的命题的序号是
17．已知函数f(x)=2+log3x，x∈[1，9]，求y=[f(x)]2+f(x2)的最值
18．已知
(1)当
时, 求证
在
内是减函数;
(2)若
在内有且只有一个极值点, 求a的取值范围.
19．已知 f (x) 是奇函数，且x < 0时，f (x) = 2 ax + ．
(1) 求x > 0时，f (x) 的表达式；
(2) a为何值时，f (x) 在 (0, 1] 上为增函数；
(3) 是否存在实数a，使 f (x) 在 (0, + ¥) 上取得最大值－9 ？
20．已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x2＋2x．
(Ⅰ)求函数g(x)的解析式；
(Ⅱ)解不等式g(x)≥f(x)－x－1；
(Ⅲ)若h(x)＝g(x)－
f(x)＋1在[－1，1]上是增函数，求实数的取值范围．
21．已知函数
． (1)求函数
的单调递减区间；
(2)若
，求证：
≤
≤x．
22．某市旅游部门开发一种旅游纪念品，每件产品的成本是15元，销售价是20元，月平均销售a件。通过改进工艺，产品的成本不变，质量和技术含金量提高，市场分析的结果表明，如果产品的销售价提高的百分率为
，那么月平均销售量减少的百分率为x2.记改进工艺后，旅游部门销售该纪念品的月平均利润是y（元）。
（1）写出y与x的函数关系式;
（2）改进工艺后，试确定该纪念品的销售价，使得旅游部门销售该纪念品的月平均利润最大.