高三一轮复习检测（集合、函数与导数之五）
1．下列函数中，在其定义域内既是奇函数又是减函数的是( )
A.
B.
C. 
D. 
2．函数
的反函数是( )
（A）
（B）
（C）
（D）
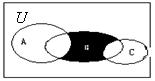3.如图，阴影部分表示的集合是
( )
（A）B∩[CU (A∪C)] （B）(A∪B)∪(B∪C)
（C）(A∪C)∩( CUB) （D）[CU (A∩C)]∪B
4.设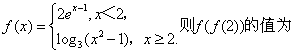
( )
A．0 B．1 C．2 D．3
5.
至少有一个负的实根的充要条件是
（ ）A．
B．
C．
D．
6.函数
的单调递增区间为
，那么实数a的取值范围是（ ）
A．
B．
C．
D．
7..若
与
在区间[1，2]都是减函数，则a的范围是( )
A.
B.
C.(0,1) D.(0,1]
8．设p：x2－x－20>0,q：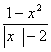
<0,则p是q的 ( )
（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件
9．3．命题“
都是偶数，则
是偶数”的逆否命题是 （ ）
A、是偶数，则都是偶数
B、不都是偶数，则不是偶数
C、不是偶数，则都不是偶数 D、 不是偶数，则不都是偶数
10．设
在
内单调递增，
，则
是
的（ ）
Ａ．充分不必要条件 Ｂ．必要不充分条件
Ｃ．充分必要条件 Ｄ．既不充分也不必要条件
11．已知定义域为R的函数
在
上为减函数，且函数
为偶函数，则（ ）
A、
B、
C、
D、
12．设函数
与
的图象的交点为
，
则
所在的区间是（ ）
A．
B．
C．
D．
13．已知函数
为奇函数，若
，
__________
14．把下面不完整的命题补充完整，并使之成为真命题.
若函数
的图象与
的图象关于 对称，则函数=
15．方程
的解为 ．
16．函数
在区间
上的最小值是 ．
17.已知定义域为
的函数
是奇函数。
（Ⅰ）求的值；
（Ⅱ）若对任意的
，不等式
恒成立，求
的取值范围；
18．已知f(x)=x2-2ax-1,x∈ [0，2]时f(x)≥a恒成立，求a的取值范围
19．已知函数f(x)满足f(logax)=
(其中a>0,a≠1,x>0).
（Ⅰ）求f(x)的表达式
（Ⅱ）判断函数的奇偶性和单调性
（III）若f(t2-2t)+ f(t) ＞0，求t的取值范围
20．已知函数f（x）＝x3＋ax2＋bx＋c在x＝－
与x＝1时都取得极值
（1） 求a、b的值与函数f（x）的单调区间
（2） 若对xÎ〔－1，2〕，不等式f（x）<c2恒成立，求c的取值范围。