直线方程、两直线的位置关系

高考能力测试步步高数学基础训练23

基础训练23　直线方程、两直线的位置关系

●训练指要

理解直线的倾斜角及斜率的含义，掌握斜率公式的三种形式，掌握直线方程的六种形式及两直线位置关系的代数条件，会求直线方程.

一、选择题

1.下列命题中是真命题的是

A.经过定点P₀(x₀，y₀)的直线都可以用方程y－y₀＝k(x－x₀)表示

B.经过任意两个不同的点P₁(x₁，y₁)、P₂(x₂，y₂)的直线都可以用方程(y－y₁)(x₂－x₁)＝(x－x₁)(y₂－y₁)表示

C.不经过原点的直线都可以用方程＝1表示

D.经过定点A(0，b)的直线都可以用方程y＝kx＋b表示

2.如果AC＜0,且BC＜0，那么直线Ax+By+C=0不通过

A.第一象限  　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.第二象限　　　　　　　　　

C.第三象限　　　　　　　　　　　　　　　　　　　　　　　　　　 D.第四象限

3.点M(1，3)，N(5，-2)，点P在x轴上，使PM－PN取最大值的点P的坐标为

A.(４，0)　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.(13，0)

C.(5，0)　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.(1，0)

二、填空题

4.已知两点A(cos70°，cos20°)、B(sin80°，sin10°)，则直线AB的倾斜角是_________.

5.已知直线ax+3y+1=0与直线x+(a-2)y+a=0，当a=_________时，两直线平行；当a＝_________时，两直线重合；当a∈_________时，两直线相交.

三、解答题

6.求分别满足下列条件的直线l的方程：

(1)直线l过点A(1，-2)，且点B(2，1)到l的距离等于1；

(2)过点M(-1，2)作直线l，使点A(-3，4)和B(1，-2)到l的距离相等；

(3)直线l过点P(-3，4)，且在两坐标轴上的截距相等.

7.一直线被两条平行直线x+2y-1=0及x+2y-3=0所截的线段的中点在直线x-y-1=0上，且这条直线与两平行线的夹角为45°，求此直线的方程.

8.已知直线l过P(-1，2)且与以A(-2，-3)，B(3，0)为端点的线段相交，求直线l的斜率的取值范围.

高考能力测试步步高数学基础训练23答案

一、1.B　2.C

3.B

提示：作N(5,－2)关于x轴的对称点N′(5,2),直线MN′与x轴的交点P即为所求.

二、4.130°

提示：k_AB=

=－cotα,

其中.

设直线AB的倾斜角为θ,

则tanθ=－cot40°=tan130°,

∴θ=130°.

5.3　－1　{aa∈R,a≠－1，且a≠3}

三、6.(1)x=1或4x－3y－10=0;

(2)x=－1或3x+2y－1=0;

(3)x+y－1=0或4x+3y=0.

7.3x－9y－1=0或9x+3y－13=0.

提示：由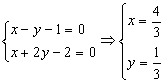即所求直线过定点().

设所求直线的斜率为k，由夹角公式得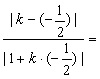=tan45°=1k=－3或k=.由点斜式求得直线方程.

8.(－∞,－

提示：因过P与x轴垂直的直线与线段AB相交，数形结合知k_l≤k_PB或k_l≥k_PAk_l≤－或k_l≥5.