直线和圆单元检测题
第Ⅰ卷（选择题 共60分）
一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）
6、直线
在y轴上的截距是－1，且它的倾斜角是直线
的倾斜角的2倍，则 （ ）
A．
B．
C．
D．
平行直线x－y＋1 = 0，x－y－1 = 0间的距离是（B）
A．
B．
C．2 D．
1.已知直线l1:x+ay+1=0与直线l2:x－2y+2=0垂直，则a的值为 D
A.2
B.－2 C.－
D.
10、
是直线
垂直的 （ ）
A．充分而不必要的条件 B．必要而不充分的条件
C．充要条件 D．既不充分又不必要的条件
26、已知直线l过点M（－1，0），并且斜率为1，则直线l的方程是（ B ）
（A） x＋y＋1＝0 （B）x－y＋1＝0 （C）x＋y－1＝0 （D）x―y―1＝0
36、直线x－ay＋
＝0（a>0且a≠1）与圆x2＋y2＝1的位置关系是（ A ）
（A）相交 （B）相切 （C）相离 （D）不能确定
44、已知定点P1（3，5），P2（－1，1），Q（4，0），点P分有向线段
所成的比为3，则直线PQ的方程是（ A ）。
(A)x＋2y－4＝0 （B）2x＋y－8＝0 （C）x－2y－4＝0 （D）2x－y－8＝0
54、已知直线l1与l2的夹角的平分线为y=x，如果l1的方程是ax＋by＋c=0(ab>0)，那么l2的方程是（ A ）。
（A）bx＋ay＋c=0 （B）ax－by＋c=0 （C）bx＋ay－c=0 （D）bx－ay＋c=0
62、如果直线y=ax＋2与直线y=3x＋b关于直线y=x对称，那么（ B ）。
（A）a=
, b=6 （B）a=, b=－6 （C）a=3, b=－2 （D）a=3, b=6
67、过定点(1, 3)可作两条直线与圆x2＋y2＋2kx＋2y＋k2－24=0相切，则k的取值范围是（ C ）。
（A）k>2 （B）k<－4 （C）k>2或k<－4 （D）－4<k<2
88、一束光线从点A(－1, 1)出发经x轴反射，到达圆C：(x－2)2＋(y－3)2=1上一点的最短路程是（ A ）。
（A）4 （B）5 （C）3
－1 （D）2
106、不论k为何实数，直线(2k－1)x－(k＋3)y－(k－11)=0恒通过一个定点，这个定点的坐标是（ B ）。
（A）(5, 2) （B）(2, 3) （C）(5, 9) （D）(－
,3)
07、方程ax＋by＋c=0与方程2ax＋2by＋c＋1=0表示两条平行直线的充要条件是（ C ）。
（A）ab>0, c≠1 （B）ab<0, c≠1 （C）a2＋b2≠0, c≠1 （D）a=b=c=2
提示：两直线平行的充要条件。
108、与三条直线y=0, y=x＋2, y=－x＋4都相切的圆的圆心是（ C ）。
(A) (1, 2
＋2) （B）(1, 3－3)（C）(1, 3－3) （D）(1, －3－3)
6、圆x2＋y2=1上的点到直线3x＋4y－25=0的距离的最小值是（ ）。
（A）6 （B）4 （C）5 （D）1
195、各点坐标为A(1, 1)、B(－1, 1)、C(－1, －1)、D(1, －1)，则“点P在y轴”是“∠APD＝∠BPC”的（A ）。
（A）充分而不必要条件(B）必要而不充分条件（C）充要条件（D）不充分也不必要条件
提示：利用四点共圆的有关知识。
若直线
（
均大于0）始终平分圆
的周长，则
的最小值是
A．4 B.
2
C. 
D.
5、当a在（－∝，0）内变化时，要使过三点O（0，0）A（－4，0）B（－2，a ）的圆的圆心在三角形AOB内（包裹边界），则a允许的最大值是（ ）
（A）－√2 （B）－1 （C） －2√2 （D） －2
9.如果直线ax+by=4与圆C：x2+y2=4有两个不同的交点，那么点（a，b）和圆C的位置关系是 A
A.在圆外 B.在圆上 C.在圆内 D.不能确定
12．将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点（－2，4）重合，若点（7，3）与点（m ,n）重合，则m+n的值为( C )
A．4 B．－4 C．10 D．－10
11、若直线
始终平分圆
的周长，则
的取值范围是（ ）
A．
； B．
； C．
； D．
11．过点
引一条直线，使它与
和
的距离相等，那么这条直线的方程是
（A）
（B）
（C）
或 （D）
或
8.若直线x+2y+m=0按向量a=(－1,－2)平移后与圆C：x2+y2+2x－4y=0相切，则实数m的值等于（ D ）
A.3或13 B.3或－13 C.－3或7 D.－3或－13
5．点M（x0，y0）是圆x2+y2=a2(a>0)内异于圆心的点，则直线x0x+y0y=a2与该圆的位置关系是 （C ）
A．相切 B．相交 C．相离 D．相切或相交
8．把直线x+y－1=0沿y轴正方向平移1个单位再关于原点对称后，所得直线的方程是（ A ）
A．x+y+2=0 B．x－y－2=0 C．x+y－2=0 D．x－y+2=0
15．直线l：x+2y-3=0与圆C：x2+y2+x-6y+m=0有两个交点A、B，O为坐标原点，若
, 则m的值是 ( B )
A．2 B．3 C．-1 D．
2、直线
与圆
的位置关系是（ ）
A、相交 B、相离 C、相切 D、相交或相切
12．台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为 （ ）
A．0.5小时 B．1小时 C．1.5小时 D．2小时
2.已知
是直线
上定点,M是平面上的动点,则
的最小值是( C )
(A)
(B) 
(C)
(D) 
8．若一个圆的圆心在抛物线
的焦点处，且此圆与直线
相切，则这个圆的方程是 （ A
）
A．
B．
C．
D．
11．写出直线
与直线
互相垂直的一个充分不必要条件 
。
14．已知直线
，
过点
，并且它们的方向向量
满足
，那么的方程是
. 14．
16．不等式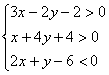
的整数解为
。
15、已知平行直线
与同心圆系
的交点为
当
取最小值时，
的取值为
. 15，
22、（14分）直线l: y=2x是△ABC中∠C的平分线所在直线，若A（-4，2），B（3，1）。
(1)求点A关于直线l的对称点D的坐标；
(2)求点C的坐标；
(3)求△ABC的高CE所在的直线方程
19．（共11分）已知直线
：
，：
，
：
。
（I）求三直线交于一点的条件；
（II）当三直线交于一点时，确定、
的值，使得直线和关于直线对称。
20、在直角坐标系中，已知点
（p>0）, 设点F关于原点的对称点为B，以线段FA为直径的圆与y轴相切.
（1） 求点A的轨迹C的方程；
（2） PQ为过F点且平行于y轴的曲线C的弦，试判断PB与QB与曲线C的位置关系.
（3）
是曲线C的平行于y轴的任意一条弦，若直线FM1与BM2的交点为M，试证明点M在曲线C上.
21．已知动圆过定点A（1，0），且与定直线l：x＝－1相切．
（1）求动圆圆心的轨迹E；
（2）过点M（t，0）（t>0）的直线m与轨迹E交于A、B两点，M关于原点的对称点为N，当
时，求弦AB在x轴上的投影的长；
（3）在（2）的条件下，若AS⊥x轴于S，求证：∠SAB＝∠SBA．