一元二次不等式的解法
一、学习目标
1.掌握一元二次不等式的解法步骤,能熟练地求出一元二次不等式的解集。
2.掌握一元二次不等式、一元二次方程和二次函数的联系。
二、例题
第一阶梯
例1什么是一元二次不等式的一般式?
【解】一元二次不等式的一般式是:
ax2+bx+c(a>0)或ax2+bx+c<0(a>0)
【评注】
1.一元二次不等式的一般式中,严格要求a>0,这与一元二次方程、二次函数只要求a≠0不同。
2.任何一元二次不等式经过变形都可以化成两种“一般式”之一,当a1<0时,将不等式乘-1就化成
了“a>0”。
例2、一元二次不等式、一元二次方程和二次函数的联系是什么?
【点拨】用函数的观点来回答。
【解】
二次不等式、二次方程和二次函数的联系是:设二次函数y=ax2+bx+c (a≠0)的图象是抛物线L,则不
等式ax2+bx+c>0,ax2+bx+c<0的解集分别是抛物线L在x轴上方,在x轴下方的点的横坐标x的集合;二次方
程ax2+bx+c=0的根就是抛物线L与x轴的公共点的横坐标。
【评注】
二次不等式、二次方程和二次函数的联系,通常称为“三个二次问题”,我们要深刻理解、牢牢掌握,
并灵活地应用它。它是函数与方程思想的应用范例。应用这“三个二次”的关系,不但能直接得到“二次
不等式的解集表”,而且还能解决“二次问题”的难题。
例3请你自己设计一张好用的“一元二次不等式的解集表”。
【解】一元二次不等式的解集表:
| 记忆图 | | ||
| 分类 | △>0 | △=0 | △<0 |
| ax2+bx+c>0 (a>0)的解集 | (-∞,x1)∪(x2,+∞) | (-∞,x0)∪(x0,+∞) | R |
| ax2+bx+c<0 (a>0)的解集 | (x1,x2) |
|
|
【评注】
1.不要死记书上的解集表,要抓住对应的二次方程的“根”来活记活用。
2.二次方程的解集求法属于“根序法”(数轴标根)。
例4、写出一元二次不等式的解法步骤。
【解】一元二次不等式的解法步骤是:
1.化为一般式ax2+bx+c>0 (a>0)或ax2+bx+c<0 (a>0)。这步可简记为“使a>0”。
2.计算△=b2-4ac,判别与求根:解对应的二次方程ax2+bx+c=0,判别根的三种情况,△≥0时求出根。
3.写出解集:用区间或用大括号表示解集。
例:解不等式 x+2>3x2
解:原不等式等价于
3x2-x-2<0
解方程3x2-x-2=0得二根:![]() ,x2=1。
,x2=1。
∴原不等式的解集为(![]() ,1)。
,1)。
第二阶梯
例1、解下列不等式:
(1)2+3x-2x2<0;
(2)-x2+2x-3x>0;
(3)x2-4x+4>0
【解】(1)原不等式等价于2x2-3x-2>0
由2x2-3x-2=0得![]() ,x2=2.
,x2=2.
∴原不等式的解集是![]()
(2)原不等式等价于:x2-2x+3<0
由△=![]() <0,知原不等式解集为
<0,知原不等式解集为![]() 。
。
(3)△=![]() ,方程
,方程![]() 有等根
有等根![]() ,
,
∴原不等式的解集为{xx∈R,且x≠2}。
【评注】
1.要严格按“解法步骤”求解。
2.最后要用集合表示法表出解集。如本倒的(1)用区间表出解集;本例之(3)用大括号表出解集,
该题的解集也可用区间表为![]() ,但有的同学把第(3)题的解集表为x≠2,这是错误的。
,但有的同学把第(3)题的解集表为x≠2,这是错误的。
例2、解不等式(1+x)(2-x)(x2+x+1)>0
【探路】化为一元二次不等式来解。
【解】∵y=x2+x+1的判别式△=12<0,a=1>0
∴对一切x∈R恒有x2+x+1>0,
∴原不等式等价于
(1+x)(2-x)>0![]() <0
<0![]() -1<x<2
-1<x<2
∴原不等式的解集为(-1,2)。
例3、设全集为R,已知A={![]() },求
},求![]() 。
。
【探路】解不等式化简集合A。
【解】![]()
![]()
![]() ,……(1)
,……(1)
方程2x2-x-1=0的两根为![]()
∴不等式①的解集为[![]() ,1],
,1],
∴A=[![]() ,1]
,1]
∴![]()
例4、已知关于x的方程2x2+4mx+3m-1=0有两个负数根,求实数m的取值范围。
【探路】列出方程有两个负根的等价条件(不等式组),然后解不等式组。
【解】已知方程有两个负根的等价条件是
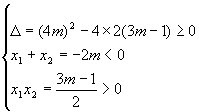
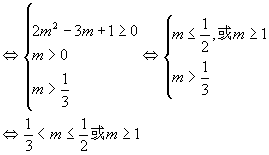
∴m的取值范围是(![]() ]∪[1,+∞)
]∪[1,+∞)
【评注】
1.方程有两个负根包含两个负根相等的情形,故△≥0,因此列成△>0是错误的。又若只列成△≥0也
是错误的,△≥0只能保证方程有实根,而不能保证有两个负根,所以还要联立x1x2>0,x1+x2<0的条件。
2.利用不等式讨论方程的根的情况,是不等式的重要应用。
第三阶梯
例5、已知A=![]() ,B=
,B=![]() 。
。
(1)若B![]() A,求a的取值范围;
A,求a的取值范围;
(2)若A∩B是单元素集合,求a取值范围。

【探路】先解不等式化简集合A和B,再利用数轴表示两个集合的关系,求a的取值。
【解】解不等式![]() 得A=[1,2];而B={
得A=[1,2];而B={![]() ≤0}。
≤0}。
(1)若B![]() A,如图1,得a的取值范围是1≤a<2。
A,如图1,得a的取值范围是1≤a<2。
(2)若A∩B是单元素集合,如图2,A∩B只能是集合{1}
∴a的取值范围是a≤1。
【评注】
集合B的最简表示只能是B={![]() },这是因为不知道a与1的大小,不能表示为最简洁的
},这是因为不知道a与1的大小,不能表示为最简洁的
区间;此外,当a=1时,集合B是单元素集合,即B={1},也不该表示为区间。
例6、解关于x的不等式2x2-5ax-3a2<0(a∈R)。
【探路】先求出不等式相应的二次方程的根,然后注意分类讨论,比较两根的大小,求出不等式的解集。
【解】解方程2x2-5ax-3a2=0,得
![]()
当a>0时,![]() <3a,原不等式的解集是(
<3a,原不等式的解集是(![]() ,3a);
,3a);
当a<0时,![]() >3a,原不等式的解集是(3a,
>3a,原不等式的解集是(3a,![]() );
);
当a=0时,![]() =3a=0,原不等式的解集是
=3a=0,原不等式的解集是![]() 。
。
【评注】解含字母系数的二次不等式,在求出相应方程的二根后,应注意对字母分类讨论两根的大小,
进而确定相应的解集。
例7已知![]() (且b>0)的解集为{x-1≤x≤2},求实数a,b的值。
(且b>0)的解集为{x-1≤x≤2},求实数a,b的值。
【探路】将不等式ax+3≤b化为二次不等式,利用二次不等式与二次方程的关系求a、b的值。
【解】![]()
![]()
∴关于x的二次不等式![]() (a2>0)的解集为[-1,2]。
(a2>0)的解集为[-1,2]。
∴-1和2是方程![]() 的二根
的二根
∴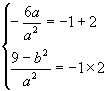
解得![]() ;或
;或![]()
∵b>0,舍去后一组解。
∴a=-6,b=9
【评注】本例就是利用一元二次不等式与一元二次方程的联系来解题。
三、练习题
A组
1.不等式x(x+1) >x(x+1)的解集是( )
(A)(-∞,-1)∪(-1,+∞) (B)(-1,+∞)
(C)(-∞,-1)∪(-1,0) (D)(-1,0)
2.不等式42x2+ax<a2(常数a<0)的解集是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
3.不等式![]() <0的解集是( )
<0的解集是( )
(A)(0,3) (B)(-3,0) (C)(-3,3) (D)R
4.若关于x的不等式ax2+bx+c<0(a≠0)的解集为![]() ,那么( )
,那么( )
(A)a<0,且b2-4ac>0 (B)a<0,且b2-4ac≤0
(C)a>0,且b2-4ac≤0 (D)a>0,且b2-4ac>0
5.有三个关于x的方程:![]() ,已知其中至少有一个方
,已知其中至少有一个方
程有实根,则实数a的取值范围为( )
(A)-4≤a≤4 (B)-2<a<4 (C)a<0 (D)a≤-2,或a≥4
6.不等式4≤x2-3x<18的整数解集是 。
7.若方程组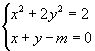 有两组解,则实数m的取值集合是
。
有两组解,则实数m的取值集合是
。
8.集合A=![]() ,B=
,B=![]() ,则A∩B=
。
,则A∩B=
。
9.若![]() 的解集是{x2<x<4},则p,q的值分别是p=
,q= 。
的解集是{x2<x<4},则p,q的值分别是p=
,q= 。
10.对任何实数x,函数![]() 的值恒为负数,则p的取值范围是
。
的值恒为负数,则p的取值范围是
。
【答案】
1.D 2.B 3.C 4.C
5.D 6.{-2,-1,4,5} 7.(![]() )
)
8.(2,4) 9. ![]() 10.-4<p≤0
10.-4<p≤0
B组
1.解不等式:
(1)(x+1)(x+2)> 0;
(2) 2x(x-![]() )< 0;
)< 0;
(3)14-4x2 ≥x;
(4)0<x2-x-2 <4.
2.解不等式组
x(x2+1)≥(x+1)(x2-x+1),
1-2x>3(x-9).
3.解不等式:
(1)![]() < 0
(2)
< 0
(2)![]() > 1
> 1
4.解不等式(x+a)(x+b)>0 (a<b)
5.X为何值时,抛物线y=-x2+5x-5上的点位于直线y=1的上方。
6.已知U=R,且A={x x2-9 <0 },B={x x2-3x+2≥ 0} 求:
(1)A∩B; (2)A∪B (3)Cu(A∩B) (4)(Cu A)∪(Cu B)
7.不等式(a2-1)x2-(a-1)x-1 <0的解集为R,求a的取值范围。
8.解不等式x>![]()
9.已知全集U=R,A={xx2-x-6>0},B={xx2+2x-8>0},C= {xx2-4ax+3a<0},若A∩BC,求实数a的取值范围。
10.已知A={xx-a≤1},B={x![]() ≥ 0},且A∩B=,求a的取值范围。
≥ 0},且A∩B=,求a的取值范围。
答案
1.(1){xx<-2或x>-1}; (2){x0<x<![]() };
(3) {x-2≤x≤
};
(3) {x-2≤x≤![]() };
(4) {x-2<x<-1 或2<x<3}
};
(4) {x-2<x<-1 或2<x<3}
2.{x1 x<![]() }
3.(1) {x-
}
3.(1) {x- ![]() <x〈
<x〈![]() 〉; (2) {x
〉; (2) {x ![]() <
x <
<
x <![]() }
4.{xx<-b 或x>-a}.
}
4.{xx<-b 或x>-a}.
5.{x2<x<3}
6.易得A=(-3,3),B=(-∞,1)∪[2,+∞],则
(1)A∩B={x-3<x≤ 1 或2 ≤x<3}
(2)A∪B=R
(3)Cu(AB)={xx ≤–3或1<x<2或x≥3}.
(4)(CuA)∪( CuB)={xx≤–3或1<x<2或x≥3}
7.当a2-1=0时a=1,有x ∈R.
当a2-1≠ 0时,
△=(a-1)2+4(a2-1)=5a2-2a-3<0
a2-1<0
即—![]() <a<1时有x∈R.
<a<1时有x∈R.
综上所述:-![]() <a≤1
<a≤1
8.x>![]() 化为
化为![]() >0,化为
>0,化为
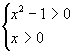 或
或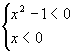 即x>1或-1<x<0,
即x>1或-1<x<0,
所以解集为{x-1<x<0或x>1}
9.A=(-2,3),B=(-∞, -4 ) (2,+∞),A ∩B=(2,3),C={x(x-a)(x-3a)<0},
当a<0时, c=(3a,a),A∩B∈C不可能成立
当a>0时,c=(a,3a),由A ∩B ∈C得
![]() 即1≤a≤2.
即1≤a≤2.
10.A=[a-1,a+1], B=[0,1]∪ (3,+∞ )
a+1<0或![]() 即a<-1.
即a<-1.
