正、余弦定理及解三角形

高考能力测试步步高数学基础训练18

基础训练18　正、余弦定理及解三角形

●训练指要

明确解斜三角形的含义，会用正、余弦定理解题.

一、选择题

1.一个三角形的两内角分别为45°和60°，如果45°角所对的边长是6，那么60°角所对的边长为

A.3　　　　　　　　　　　　B.3　　　　　　　C.3　　　　　　　　 D.2

2.在△ABC中，若∠A∶∠B∶∠C=1∶2∶3,则a∶b∶c等于

A.1∶2∶3　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.3∶2∶1

C.2∶∶1　　　　　　　　　　　　　　　　　　　　　　　　　D.1∶∶2

3.在△ABC中，∠A=60°,a=,b=4,满足条件的△ABC

A.无解　　　　　　　　　　　　 B.有解　　　　　　　　　　　　 C.有两解　　　　　　　　　　 D.不能确定

二、填空题

4.在△ABC中，若三边的长为连续整数，且最大角是最小角的二倍，则三边长分别是_________.

5.△ABC中，已知∠A∶∠B＝1∶3，角C的平分线将三角形面积分成5∶2，则sinA＝_________.

三、解答题

6.已知△ABC中，a=8,b=7,B=60°，求边c及S_△ABC.

7.已知△ABC的面积为1，tanB=,tanC=-2,求△ABC的三边及△ABC的外接圆直径.

8.(2001年全国高考题)已知圆内接四边形ABCD的边长分别为AB=2，BC=6，CD=DA=4，求四边形ABCD的面积.

高考能力测试步步高数学基础训练18答案

一、1.A

2.D

提示：设∠A=α,∠B=2α,∠C=3α,则α+2α+3α=180°，α=30°,

∴∠A=30°,∠B=60°,∠C=90°,

a∶b∶c=sin30°∶sin60°∶sin90°　=

3.C　

二、4.4，5，6

提示：设三边长分别为x－1,x,x+1(x∈N*且x＞1)，最大角为C，最小角为A，

则cosC=

C=2A,∴cosC=2cos²A－1,求得x=5,三边长为4，5，6.

5.

提示：,

∴2sin3A=5sinA,2(3sinA－4sin³A)=5sinAsinA=.

三、6.c=5,S_△ABC=10或c=3，S_△ABC=6

7.a=

提示：求得sinA=,设外接圆半径为R，由正弦定理知a=

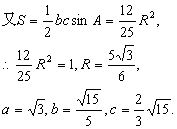
8.8.

提示：连结BD，S_{四边形ABCD}=S_△ABD+S_△CDB=…=16sinA.

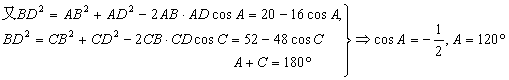
∴S_{四边形ABCD}=8.