当前位置：首页 -高中数学试卷 - 高中三年级数学试题 - 正文*

直线

2014-5-11 0:19:46下载本试卷

学科：数学

教学内容：直线

一、考纲要求

1.理解有向线段的概念.掌握有向线段定比分点坐标公式，熟悉运用两点间的距离公式和线 段的中点坐标公式.

2.理解直线斜率的概念，掌握过两点的直线的斜率的公式，熟练掌握直线方程的点斜式，掌 握直线方程的斜截式、两点式、截距式以及直线的一般式.能够根据条件求出直线的方程.

3.掌握两条直线平行与垂直的条件.能够根据直线的方程判定两条直线的位置关系.会求两条 直线的夹角和交点.掌握点到直线的距离公式.

二、知识结构

1.有向线段

一条有向线段的长度，连同表示它的方向的正负号，叫做有向线段的数量.有向线段的数量用AB表示.

若有向线段在数轴上的坐标为A(x1)，B(x2)，则

它的数量　　AB=x2-x1

它的长度　　｜AB｜=｜x2-x1｜

平面上两点间的距离　设P1(x1,y1),P2(x2,y2)是坐标平面上的任意两点，则 它们的距离

｜P1P2｜=

当P1P2⊥Ox轴时，｜P1P2｜=｜y2-y1｜；当P1P2⊥Oy轴时，｜P1P2｜ =｜x2-x1｜；点P(x,y)到原点O的距离，｜OP｜=.

三角形的中线长公式

如图，AO是△ABC的BC边上的中线.则｜AB｜2+｜AC｜2

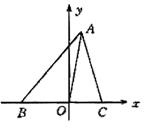
=2［｜AO｜2+｜OC｜2］

2.线段的定比分点

有向直线l上的一点P，把l上的有向线段分成两条有向线段分成两条有向线段，则和的数量之比

λ=

定比分点公式　若P1、P2两点坐标为(x1,y1)，(x2,y2),点P(x,y)分有向线段成定比

λ= (λ≠-1)，

则P点坐标

x=，　　y=.

(1).中点公式　设P1(x1,y1),P2(x2,y2)，则P1P2的中点P(x,y)的坐标是

x=,　　y=.

(2)三角形的重心公式　若△ABC的各顶点坐标分别为A(x1,y1),B(x2,y2),C(x3,y 3)，则△ABC的重心G(x,y)的坐标是

x=，　　　y=

3.直线的方程

直线方程的几种形式

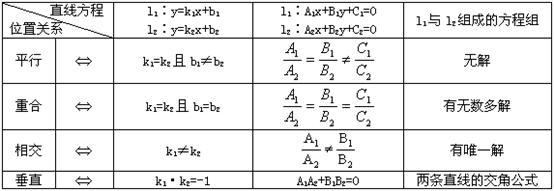
名称

已知条件

方程

说明

斜截式

斜率k纵截距b

y=kx+bx

不包括y轴和平行于y轴的直线

点斜式

点P 1(x1,y1)斜率k

y-y1=k(x-x1)

不包括y轴和平行于y轴的直线

两点式

点P1(x1,y1)和P2(x2,y2)

不包括坐标轴和平行于坐标轴的直线

截距式

横截距a纵坐标b

=1

不包括坐标轴，平行于坐标轴和过原点的直线

一般式

—

Ax+By+C=0

A、B不同时为0

两条直线的位置关系

当直线不平行于坐标轴时：

(1)直线l1到l2的角　直线l1依逆时针方向旋转到与l2重合时所转的角，叫做l1 到l2的角.

计算公式

设直线l1，l2的斜率分别是k1，k2，则

tgθ=　　  (k1k2≠-1)

(2)两条直线的夹角一条直线到另一条直线的角小于直角的角，即两条直线所成的锐角叫做两条直线所成的角，简称夹角.这时的计算公式为：tgθ=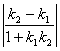

4.点与直线的位置关系

点P(x0,y0)在直线Ax+By+C=0上的充要条件是

Ax0+By0+C=0.

点到直线的距离公式

点P(x0,y0)到直线Ax+By+C=0的距离是

d=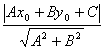

据此可推出：

(1)两平行线间的距离公式

两平行直线Ax+By+C1=0和Ax+By+C2=0间的距离为

d=.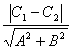

5.直线关于点的对称

直线关于点的对称直线一定是一条与已知直线平行的直线，由中点坐标公式可得

直线Ax+By+C=0关于点P(x0,y0)的对称直线方程是

A(2x0-x)+B(2y0-y)+C=0

即　　　　 　　　　　　　　　Ax+By-(2Ax0+2By0+C)=0.

“直线关于直线”对称

(1)几种特殊位置的对称

已知曲线f(x,y)=0，则它：

①关于x轴对称的曲线是f(x,-y)=0；

②关于y轴对称的曲线是f(-x,y)=0；

③关于原点对称的曲线是f(-x,-y)=0；

④关于直线y=x对称的曲线f(y,x)=0；

⑤关于直线线y=-x对称的曲线

f(-y,-x)=0；

⑥关于直线x=a对称的曲线是

f(2a-x,y)=0；

⑦关于直线y=b对称的曲线是

f(x,2b-y)=0

三、知识点、能力点提示

(一)有向线段、两点间距离、线段的定比分点

例1　在△ABC中，A(4，1)，B(7，5)，C(-4，7)，求∠BAC平分线的长.

解：　由两点距离公式求得│AB│=5，│AC│=10，设角平分线交BC于D(x，y)，由角平分线性质得λ=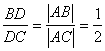，从而求得D(，)，故可得│AD│=.

(二)直线方程，直线的斜率，直线的点斜式、斜截式、两点式、截距式方程，直线方程的一 般形式

例2　直线xcosα-y+1＝0的倾斜角的变化范围是　　　　　　　　　　　 .

解　直线方程化为斜截式y=cosα·x+1，故k=cosα，

又-1≤k≤1，故倾角所取范围是［0，］和［，π］。

(三)两条直线平行与垂直的条件，两条直线所成的角，两条直线的交点，点到直线的距离

说明　这部分内容近年高考在填空、选择及解答题中都常考查到.

使用公式求l1到l2的角时，应注意k1、k2的顺序.过两直线交点的直线系方程中不 包括直线l2.

例3　光线由点(-1，4)射出，遇直线2x+3y-6=0被反射，已知反射光线过点(3 ，).求反射光线所在直线方程.

解：　设(-1，4)点关于已知直线对称点为(x′，y′).

则点(-1，4)与点(x′，y′)的连线段被已知直线垂直平分，故可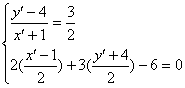得　解得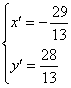，再由两点式可得所求直线方程为13x-26y+85=0.

(四)综合例题赏析

例4设点P在有向线段AB的延长线上，P分AB所在的比为λ，则　(　　)

A.λ＜-1　　　　　  B.-1＜λ＜0

C.0＜λ＜1　　　　  D.λ＞1

解　由已知有λ＝因为与的方向相反，且｜｜＞｜｜，

所以λ＝｜｜＜-1，

应选A。

例5　和直线3x-4y+5=0关于x轴对称的直线方程是(　　)

A.3x+4y-5=0 　　　　　B.3x+4y+5=0

C.-3x+4y-5=0　　　　  D.-3x+4y+5=0

解：　若曲线c的方程f(x,y)=0，曲线c和c′关于x轴对称，则曲线c′的方程是f(x，-y)=0.

∴3x-4(-y)+5=0即3x+4y+5=0为所求.

应选B.

例6　如图，设图中直线l1，l2，l3的斜率分 别为k1，k2，k3，则(　　)

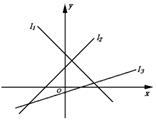
A.k1＜k2＜k3　　　　  B.k3＜k1＜k2

C.k3＜k2＜k1　　　　  D.k1＜k1＜k2

解　显然k1＜0，0＜k3＜k2

于是应选D.

例7　如果直线y=ax+2与直线y=3x-b关于直线y=x对称，那么(　　)

A.a=,b=6　　　　  B.a=,b=-6　　　　 C.a=3,b=-2　　　　  D.a=3,b=6

解　C1的方程是f(x,y)=0,C2和C1关于直线y=x对称，则C2的方程是f(y,x)=0.

于是直线y=ax+2关于直线y=x对称的直线的方程是x=ay+2,即y=.

由题设y=和y=3x-b是同一条直线，

所以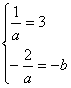，解得

从而应选A.

例8　通过点(0，2)且倾斜角为15°的直线方程是(　　)

A.y=(-2)x+2　　　　  B.y=(-1)x+2

C.y=(2-)x+2　　　　  D.y=(-1) x+2

解：　∵直线通过点(0，2).

∴直线在y轴上的截距b=2.

∵直线的倾角为15°，

∴直线的斜率k=tg15°=.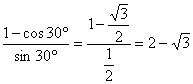

把k=2-，b=2代入直线的斜截式方程y=kx+b，得y=(2-)x+2 .

应选C.

例9　直线3x-2y=6在y轴上的截距是(　　)

A.　  B.-2　　C. -3　　D.3

解：　∵3x-2y=6y=-+=1，

又直线的截距为=1，

∴b=-3，即在y轴上的截距为-3.

应选C.

例10　如果直线ax+2y+2=0与直线3x-y-2=0平行，那么 系数a=(　　)

A.-3　  B.-6　　C.-　　D.

解：l1:A1x+B1y+C1=0，l2:A2x+B2y+C2=0，且A2≠0，B2≠0，C2≠ 0，则有

l1∥l2

∴由题设有=a=- 6.

应选B.

例11　两条直线A1x+B1y+C1=0,A2x+B2y+C2=0垂直的充要条件是 (　　)

A.A1A2+B1B2＝0　　　　  B.A1A2-B1B2＝0

C.＝-1　　　　  D.

解　若B1B2＝0，不妨设B1＝0，则直线l1∶A1x+C1=0，l1是垂直与x轴的直 线，由于l1⊥l2，所以l2是垂直y轴的直线，从而l2∶B2y+C2=0，即A2=0

故　A1A2+B1B2＝0

若B1B2≠0，则l1和l2的方程可化为y=-,y=-,得k1＝-，k2＝-,

由l1⊥l2k1·k2=-1·＝-1A1A2+B1B2＝0.

综上有若l1⊥l2，则A1A2+B1B2＝0

反之，若A1A2+B1B2＝0

1°A1A2≠0B1B2≠0A1A2＝-B1B2＝-·

＝-1()·()＝-1，

即k1·k2＝-1

所以l1⊥l2.

2°若A1·A2＝0，不妨设A1＝0，且A2≠0，则B1≠0且B1·B2＝0B2＝0 ，

所以l1∶B1y+C1=0,是垂直y轴的直线；

　　l2∶A2x+C2=0,是垂直x轴的直线；

于是l1⊥l2

又若A1＝0且A2＝0则l1∶B1y+C1=0,l2∶B2y+C2=0,则l1∥l2，此与

l1⊥l2矛盾.

综上有　若A1A2+B1B2＝0，则l1⊥l2

综合(1)、(2)知，l1⊥l2A1A2＝B1B2＝0

故应选A.

例12　如果直线ax+2y+1=0与直线x+y-2=0互相垂直，那么a 的值等于(　　)

A.1　　B.-　　C. -　　D.-2

解：两直线l1:A1x+B1y+C1=0，l2:A2x+B2y+C2=0，互相垂直的充要条件是 ：

A1A2+B1B2=0

∴由题设得a·1+2·1=0，从而a=-2.

应选D.

例13　点P(2，5)关于直线x+y=0的对称点的坐标是(　　)

A.(5，2)　　　　　  B.(2，-5)

C.(-5，-2)　　　　　D.(-2，-5)

解：设P(2，5)和Q(m，n)关于直线y=-x对称，则PQ中点R(，)在y=-x上，且KPQ·(-1)=-1.

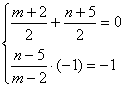∴，解得

∴对称点Q的坐标是(-5，-2).

应选C.

例14　原点关于直线8x+6y=25的对称点坐标是(　　)

A.(2，) 　　　　　 B.(，)

C.(3，4)　　　　 　　D.(4，3)

解：设(m，n)为所求，则

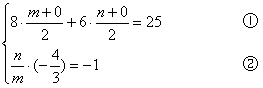
解得m=4，n=3

∴应选D.

例15　在直角坐标中，△ABC的三个顶点是：A(0，3)，B(3，3)，C(2 ，0)，若直线x=a，将△ABC分割成面积相等的两部分，则实数a的值是(　　)

A.　 　 B.1+　　  C.1+　　  D.2-

解　如图

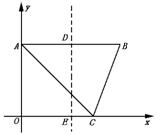
易知直线AC的方程是y=3，直线AC的方程是＝1，即3x+ 2y=6.

设直线x=a与AB交于D，与AC交于E，则D，E的坐标分别为D(a,3),E(a,)

从而｜DE｜=3-=a

S△ADE＝AD·DE＝a·a=a2　　　　  (1)

又S△ABC＝·3·＝，

S△ADE＝·S△ACB＝，　　　　　　　　　　(2)

由(1)，(2)有a2＝，解得a=

应选A.

例16　以A(1，3)、B(-5，1)为端点的线段垂直平分线的方程是(　　)

A.3x-y+8=0　　　　  B.3x+y+4=0

C.2x+y+2=0　　　　  D.3x+y+8=0

解：设P(x，y)为线段AB的中垂线上的点，

则│PA│=│PB│

即，化简得3x+y+4= 0.

应选B.

例17　在直角坐标系xoy中，过点P(-3，4)的直线1与直线OP的夹角为45°， 求1的方程.

解：设1的斜率为k，kOP=-，

∴tg45°=││=││=││，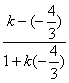

得=±1，解出k=-，7

∴1的方程为y-4=-(x+3)或y-4=7(x+3).

即1的方程为x+7y-25=0或7x-y+25=0.

例18　点(0，1)到直线x+y=2的距离是　　　　　  .

解：d=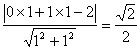

【同步达纲练习】

 (一)选择题

1.直线Ax+By+C=0通过第一、二、三象限，当且仅当(　　)

A.A·B＞0，A·C＞0 　　　　 B.A·B＞0，A·C＜0

C.A·B＜0，A·C＞0　　　　  D.A·B＜0，A·C＜0

2.已知点M(3，4)，N(12，7)，P在直线MN上，且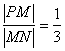，则点P的坐标是(　　)

A.(6，5)　　　　　　  B.(9，6)

C.(0，3)　　　　　　  D.(0，3)或(6，5)

3.已知点A(3，3)，B(-1，5)，直线y=ax+1与线段AB有公共点，则实数a应满足的条件是(　　)

A.a∈［-4，］　　　　  　　　　　　 B.a≠-

C.a∈［-4，］∪(-，)　　　　  D.a∈(-∞，-4)∪(，+∞］

4.方程│x-1│+y=1确定的曲线与x轴围成的图形的面积是(　　)

A. 　　　B.1　　　C.2　　　D.4

5.过点(2，3)且在两坐标轴上截距相等的直线方程是(　　)

A.x+y=5　　　　　　　  　　B.3x-2y=0

C.x+y=5或3x-2y=0　　　　  D.4x-y=5

6.直线l过点P(3，2)，与x轴、y轴的正半轴交于A、B两点，O是坐标原点，当△AOB面积为最 小值时，直线l的方程是(　　)

A.x-y-1=0　　　　　　　　  B.x+y-5=0

C.2x+3y-12=0　　　　　　　 D.3x+2y-13=0

7.如果直线Ax+By+C=0的倾斜角是一锐角，且在y轴上的截距大于零，则(　　)

A.AB＞0，AC＞0　　　　 　 B.AB＞0，AC＜0

C.AB＜0，AC＞0　　　　 　 D.AB＜0，AC＜0

8.下列各点中，不与P(4，3)、Q(-1，6)两点共线的点是(　　)

A.(5，6)　　　　  　　　　B.(2，-3)

C.(3t，t+3)(这里t∈Z)　　 D.(t+3，3t)(这里t∈Z)

9.两条不重合的直线mx+y-n=0和x+my+1=0互相平行的充要条件是(　　)

A.m=1，n=1　　　　　　　  B.m=-1，n=-1

C.m=1,n≠-1,或m=-1,n≠1　 D.m≠±1，n≠±1

10.与直线2x+3y-6=0关于点(1，-1)对称的直线是(　　)

A.3x-2y+2=0　　　　  B.2x+3y+1=0

C.3x-2y-12=0　　　　 D.2x+3y+8=0

11.已知0≤θ≤，且点(1，cosθ) 到直线xsinθ+ycosθ=1的距离等于 ，则θ等于(　　)

A. 　　　B. 　　　C. 　　　D.

12.已知直线l1∶x-2y-6=0，l2∶3x-y+4=0下列说法中错误的是(　　)

A.l1与l2的夹角是45°  　　　　B.l1到l2的角是45°

C.l2到l1的夹角是45°　　　　  D.l2到l1的角是135 °

13.若a2+b2=c2，则直线ax+by+c=0被圆x2+y2=2所截的弦长等于(　　)

A.1　　　  B.2　　　　C.　　　　D.2

14.△ABC中，B(-a,0)、C(a,0)，且两底角的正切的乘积为定值k(k＞0)，则顶点A的轨迹方 程是(　　)

A.kx2+y2=ka2(y≠0)　　　　  B.kx2-y2=ka2(y≠0)　　

C.x2+ky2=ka2(y≠0)　　　　  D.x2-ky2=ka2(y≠0)

15.设点A(-1，2)，B(2，-2)，C(0，3)，且M(a，b)是线段AB上的一点(a≠0)，则直线MC的 斜率的取值范围是(　　)

A.［-，1］　　　　　　 B.［-1， ］

C.［-，0］∪(0，1)　　  D.(-∞ ，-)∪〔1，+∞〕

(二)填空题

16.两条平行直线2x-7y+8=0和2x-7y-8=0间的距离是　　　　　　　　　 .

17.如果直线l1、l2的斜率分别是二次方程x2-4x+1＝0的两根，那么l1与l2所成 角的大小是　　　　　　　　　　 .

18.直线y=-x+b和5x+3y-31=0的交点在第一象限，那么b的范围是　　　　　　 .

19.已知点P是直线l上一点，将直线l绕点P沿逆时针方向旋转角α(0°＜α＜90°，所得直 线的方程是x-y-2=0，若将它继续为转90°-α，所得直线的方程2x+y-1=0，则直线l的方程为　　　　　  .

(三)解答题

20.正方形中心为G(-1，0)，一边所在直线的斜率为3，且此正方形的面积为14.4，求这正方 形各边所在直线的方程.

21.已知在△ABC的边上运动的点D、E、F在t=0时分别从A、B、C出发，各以一定的速度向B、 C、A前进，在t=1时分别达到B、C、A，试证明在运动过程中，△DEF的重心是一个定点.

22.一条光线从点M(5，3)射出，被直线l∶x+y=1反射，入射光线到直线l的角为β，已知tgβ=2，求入射光线与反射光线所在直线的方程.

23.用解析法证明三角形内角平分线性质定理.

24.已知点P(6，8)，过P点作直线PA⊥PB分别交x轴正半轴、y轴正半轴于A、B两点。

①求线段AB的中点的轨迹。

②若△AOB面积等于△APB面积，求此时直线PA与直线PB的方程。

25.已知动点P(x,y)在以A(π，0)、B(-，-)为两端点的线段上移动，且sinx+sin2y=0。求点P的坐标。

参考答案

【同步达纲练习】

 (一)1.C　2.D　3.D  4.B　5.C　6.C  7.D　8.C　9.C  10.D　11.A　 12.C　13.B　14.A　15.D　

(二)16.； 17.；18.＜b＜；19.略

(三)20.3x-y+9=0,3x-y-3=0,x+3y+7=0,x+3y-5=0;21，证略：22.入射光线：y -3x+12=0,反射光线：3y-x+10=0;23.证略；24.(1)3x+4y-25=0第一象限内的部分；(2)

PA∶x=6，PB∶y＝8或PA∶24x+7y-200=0，PB∶7x-24y+150＝0　25.(π，-)或(π，0).