数学学科综合能力训练(二)

	学科：数学
	教学内容：数学学科综合能力训练(二)

【同步达纲练习】

一、选择题(1-10小题,每题4分，11—14小题每题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的)

1.如图，I是全集，M、P、S是I的3个子集，则阴影部分所表示的集 合是(　　)

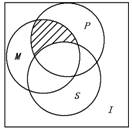
A.(M∩P)∩S

B.(M∩P)∪S

C.(M∩P)∩

D.(M∩P)∪

2.函数y=sin(cosx)的值域为(　　)

A.［-1，1］　　  B.［sin1，1］　　  C.［0，sin1］　　  D.［-sin1，sin1］

3.已知：m、n是两条直线，α、β是两个平面，则下列四个命题

(1)若m⊥n，m⊥α，则n∥α.　　　 　　　 (2)若m∥α，α⊥β，则m⊥β.

(3)若m⊥n，m⊥α，n⊥β，则α⊥β.　　　 (4)若m⊥β，α⊥β，则m∥α或mα.

其中正确命题的个数是(　　)

A.1个　　　　B.2个　　　　C.3个　　　　D.4个

4.函数y=(x-1)的反函数图象是(　　)

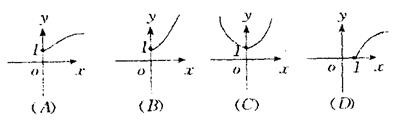
5.直线x+y-2=0截圆x²+y²=4得的劣弧所对的圆心角为 (　　)

A.　　  B. 　　　C. 　　　D.

6.复数z=sinθ-icosθ(＜θ＜π的辐角主值是(　　)

A.θ-　　  B.π-θ　　　C.2π-θ　　　D. -θ

7.(理)若＜x＜π，则arcsin()的值为(　　)

A.x+　　　　　　　　　　　B. -x

C. -x　　　　 　　　　　 D.x-

(文)已知：sinα·cosα=，且＜α＜，则cosα-sinα的值为(　　)

A.　　 B.　　 C.　　 D.

8.若棱台上下底面积分别为S₁、S₂(S₁＜S₂，则棱台的高与截得它的棱锥的高之比 为(　　)

A.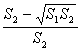　　 　　　　　B.

C.　　  　　　　　　 D.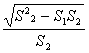

9.停车场划出一排12个停车位置，今有8辆车需要停放，要求空车位连在一起，不同的停车 方法有：

A.P⁸₈种　　　　  B.P⁸₁₂种　　　　C.P⁸₈·C¹₈种　　　　  D.P⁸₈·C¹₉种

10.一组实验数据如下表：

t	1.02	1.99	3.01	4.0	5.1	6.12	……
v	0.01	1.5	4.04	7.5	12	18.01	……

则下列四个关系式中，最接近实验数据的表达式为(　　)

A.v=log₂t　　　　 　　　　　　 B.t·2^v=1

C.v=　　　　　 　　　　　D.v+2=2t

11.若(2x+)⁴=a₀+a₁x+a₂x²+a₃x³+a₄x⁴，则(a₀+a₂+a₄)²-(a₁+a₃)²的值为(　　)

A.1　　　  B.-1　　　  C.0　　　　D.2

12.已知圆的方程为x²+y²+2(a-1)x+a²-4a+1=0(0＜a＜，则点 (-1，-1)的位置是(　　)

A.在圆上　　　　  　　　　B.在圆内

C.在圆外　　　　 　　　　 D.不能确定

13.把函数y=log_a(x-1)(a＞0且a≠1)的图象先向右平移2个单位，再把横坐标变为原来的，所得图象的函数解析式为(　　)

A.y=log_a(x-2)　　　　  B.y=log_a(x-3)

C.y=log_a(x-4)　　　　  D.y=log_a(x-2)

14.如果圆台的上底面半径为5，下底面半径为R，中截面把圆台分为上、下两个圆台，它们 的侧面积的比为1∶2，那么R＝(　　)

A.10　　　  B.15　　　  C.20　　　  D.25

二、填空题(本大题共4小题，每小题4分，共16分)

15.设椭圆=1(a＞b＞0)的右焦 点为F₁，右准线为l₁。若过F₁且垂直于x轴的弦的长等于点F₁到l₁的距离，则椭 圆的离心率是　　　　　　  .

16.不等式的解集为　　　　　　 .

17.在一块并排10垄的田地中，选择2垄分别种植A、B两种作物，每种作物种植一垄，为有利 于作物生长，要求A、B两种作物的间隔不小于6垄，则不同的选垄方法共有　　 种(用数字作答).

18.下列命题：

(1)如果平面γ与两个平面α、β所成的二面角都是直二面角，则α∥β.

(2)函数y=sinx在第一象限是增函数.

(3)函数y=tg-ctg的最小正周期是π.

(4)奇函数y=f(x)在定义域R上满足f(1+x)=f(1-x)，则y=f(x)是以4为周期的周期函数.

其中正确命题的序号是　　　　　　 .

三、解答题(本大题共6小题，共74分)

19.已知：tgx·tgy=，tg=，求cos2(x-y) 的值.

20.已知m∈C，关于x的一元二次方程x²-mx+4+3i=0恒有非零实根，且当x=a(a∈R，a≠0) 时，│m│取得最小值，记z=5-│a│i，求复数·(1-bi)(b≥1)的 辐角主值的取值范围.

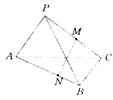
21.已知三棱锥P—ABC中，PA=PB，CB⊥平面PAB，M为PC的中点，AN=3NB.

(1)求证：MN⊥AB；

 (2)当∠APB=90°，BC=2，AB=4时，求MN的长；

(3)在(2)条件下，求PA与MN所成的角.

22.已知函数y=f(x)的图象是自原点出发的一条折线，当n≤y≤n+1(n=0,1,2,…)时，该图象是斜率为bⁿ的线段(其中正常数b≠1)，设数列｛x_n｝由f(x_n)=n(n=1,2,…)定义. (Ⅰ)求x₁、x₂和x_n的表达式；

(Ⅱ)求f(x)的表达式，并写出其定义域；

 (Ⅲ)证明：y=f(x)的图象与y=x的图象没有横坐标大于1的交点.

23.某汽车队今年(1999年)初用98万元购进一辆大客车，并投入营运，第一年需缴各种费用1 2万元，从第二年开始包括维修费内，每年所缴费用均比上一年增加4万元，该车投入营运后 每年的票款收入为50万元，设营运n年该车的盈利额为y(万元).

(1)求出y表示为n的函数关系式；

(2)从哪一年开始，该汽车开始获利(即盈利为正值)?

(3)营运若干年后，对该汽车的处理方案有两种：①当年平均盈利达到最大值时，以30万元 的价格处理该车；②当盈利额达到最大值时，以12万元的价格处理该车；问用哪种方案处理 该车较为合算?为什么?

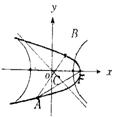
24.如图，双曲线C₁的一条渐近线是l:x+y=0，抛物线C₂的顶点是双曲线的右焦点且开口 向上，C₂上两点A与B关于l对称且∠AFB=90°，若│AB│=2，求C₁和C₂的方程.

参考答案

【同步达纲练习】

一、C　D　C  B　C　A  C　A　D  C　A　C  A　D

二、15. 　16.0＜x＜log₂3　17.12　18. ③④

三、19.(略解)tgx·tgy=

=

∴cos(x-y)=cos(x+y)

由万能公式，cos(x+y)=，cos(x-y)=，

∴cos2(x-y)=2cos²(x-y)-1=.

20.(略解)设x₀为非零实数，由已知可得：│m│=│x₀+i│=≥=3.

当且仅当x₀=±时，│m│取最小值，│a│=.

∴z=5-5i，∴(1-bi)=(5+5b)+(5-5b)i

①当b=1时， (1-bi)=10，辐角主值为0.

②当b＞1时， (1-bi)的实部大于0，虚部小于0.其辐角主值在(，2π)内，此时，arg〔(1-bi)〕=2π+arctg(-1)

∵b＞1，∴-1＜-1＜0，∴-＜arctg(-1)＜0，∴＜arg〔 (1-bi)〕＜2π.

21.(1)略  (2)MN=　(3)PA与MN所成角为60°.

22. (Ⅰ)解　依题意f(0)=0,又由f(x₁)=1,当0≤y≤1，函数f=f(x)的图象是斜率为b⁰=1的线 段，故由

＝1得x₁=1

又由f(x₂)＝2，当1≤y≤2时，函数y=f(x)的图象是斜率为b的线段，故由

＝b,即x₁-x₂＝ 得x₂＝1+.

记x₀＝0，由函数y=f(x)图象中第n段线段的斜率为b^n-1，故得

＝b^n-1

又　f(x_n)=n,f(x_n-1)=n-1；

x_n-x_n-1=()^n-1,n=1,2,…

由此知数列｛x_n-x_n-1｝为等比数列，其首项为1，公比为

因b≠1，得

x_n=(x_k-x_k-1)=1++…+=,

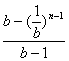即　x_n=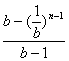

(Ⅱ)解　当0≤y≤1，从(Ⅰ)可知y=x,即当0≤x≤1时，f(x)=x

当n≤y≤n+1时，即当x_n≤x≤x_n+1时，由(Ⅰ)可知

(Ⅲ)证法一　首先证明当b＞1，1＜x＜时，恒有f(x)＞x成立

用数学归纳法证明：

(ⅰ)由(Ⅱ)知当n=1时，

在(1，x₂］上，y=f(x)=1+b(x-1)

所以f(x)-x=(x-1)(b-1)＞0成立

(ⅱ)假设n=k时在(x_k,x_k+1］上恒有f(x)＞x成立.

可得f(x_k+1)=k+1＞x_k+1

在(x_k+1,x_k+2］上，f(x)=k+1+b^k+1(x-x_k+1)

所以f(x)-x=k+1+b^k+1(x-x_k-1)-x

　　　　  =(b^k+1)(x-x_k+1)+(k+1-x_k+1)＞0也成立

由(ⅰ)与(ⅱ)知，对所有自然数n在(x_n,x_n+1)上都有f(x)＞x成立.

即　1＜x＜时，恒有f(x)＞x.

其次，当b＜1，仿上述证明，可知当x＞1，恒有f(x)＜x成立.

故函数y=f(x)的图象与y=x的图象没有横坐标大于1的交点.

证法二　首先证明当b＞1，1＜x＜时，恒有f(x)＞x成立.

对任意的x∈(1, ),存在x_n,使x_n＜x≤x_n+1，此时有

f(x)-f(x_n)=bⁿ(x-x_n)＞x-x_n(n≥1)，

f(x)-x＞f(x_n)-x_n

又f(x_n)=n＞1++…+=x_n，

f(x_n)-x_n＞0，

f(x)-x＞f(x_n)-x_n＞0，

即有f(x)＞x成立.　　　　　　　　　　　　　　　　　　　　　　　

其次，当b＜1，仿上述证明，可知当x＞1时，恒有f(x)＜x成立.

故函数f(x)的图象与y=x的图象没有横坐标大于1的交点.

23.(1)y=-2n²+40n-98；

(2)10-＜n＜10+　∵n∈N，∴3≤n≤17，故从2001年开始获 利；

(3)①=-2n+40-≤12，当且仅当n=7，即到2005年年平均盈 利达到最大值，共获利2×7+30=114万元.

②y=-2(n-10)²+102，当n=10时，y_max=102，即到2008年共获利102+12=114万元， 故两种方案获利相同，但方案②的时间长，所以用方案①处理合算.

24.C₁;x²-y²=1

C₂:y²=-(x-)

或C₁:x²-y²=

C₂:y²=-·(x-).