|
|
学科:数学 |
| 教学内容:数学学科综合能力训练(一) |
【同步达纲练习】
一、选择题(本大题共14小题,第1—10小题每小题4分,第11—14题每小题5分, 共60分)
1.已知集合A={x│![]() ≤1},B={x│log4(x+m)< 1},若A∩B=
≤1},B={x│log4(x+m)< 1},若A∩B=![]() ,则实数m的取值范围是:( )
,则实数m的取值范围是:( )
A.1<m<2 B.1≤m<2
C.1<m≤2 D.1≤m≤2
2.设集合A中含有4个元素,B中含有3个元素,现建立从A到B的映射f:A→B,且使B中的每个 元素在A中都有原象,则这样的映射f:A→B的个数为( )
A.36 B.72 C.34 D.43
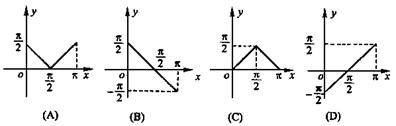
3.如图,函数y=arcsin(cosx)在0≤x≤π上的图象是( )
4.设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线sinA·x+ay+c=0与bx-sinB ·y+sinC=0的位置关系是( )
A.平行 B.重合
C.垂直 D.相交但不垂直
5.三棱锥“三条侧棱两两垂直”是“顶点在底面上的射影是底面三角形的垂心”的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知抛物线y2=2px(p>0)的焦点在直线y=x-2上滑动,对称轴作平行移动,当抛物线的 焦点移到(2a,4a+2)时,则此抛物线方程为( )
A.(y+6)2=8(x+6) B.(y-6)2=8(x-6)
C.(y-6)2=8(x+6) D.(y+6)2=8(x-6)
7.已知数列{an}的前n项和为Sn,且满足loga(Sn+a)=n+1(a>0且a≠1),则![]() 的值为( )
的值为( )
A.1 B.-1 C.-1或1 D.不存在
8.已知直线l1的参数方程为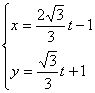 (t为参数),直线l2的极坐标方程为ρsin(θ-
(t为参数),直线l2的极坐标方程为ρsin(θ-![]() )=
)=![]() ,则l1与l2的夹角为( )
,则l1与l2的夹角为( )
A. ![]() B.
B.
![]()
C.arctg![]() D.arctg
D.arctg![]()
9.设an是(1+x)n(n=2,3,…)展开式中xn项的系数,则![]() (
(![]() +
+![]() +…+
+…+![]() )等于( )
)等于( )
A.0 B.1 C.2 D.4
10.设方程cos2x+![]() sin2x=a+1在[0,
sin2x=a+1在[0,![]() ]上有两不同的实 数解,则a的取值范围为( )
]上有两不同的实 数解,则a的取值范围为( )
A.[-3,1] B.(-π,1)
C.(0,1) D.[0,1]
11.已知椭圆![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线![]() =1和抛物线y2=2px(p>0 )的离心率分别为e1、e2、e3,则( )
=1和抛物线y2=2px(p>0 )的离心率分别为e1、e2、e3,则( )
A.e1e2>e3 B.e1e2=e3 C.e1e2<e3 D.e1e2≥e3
12.由函数y=![]() x+2和y=│x-2│的图像围成的图形绕x轴旋转一周所得旋转体的 体积是( )
x+2和y=│x-2│的图像围成的图形绕x轴旋转一周所得旋转体的 体积是( )
A.![]() B.64π C.
B.64π C. ![]() D.72π
D.72π
13.过双曲线(x-1)2-![]() =1的右焦点作直线l交双曲线于A、B两点,若│AB │=4,则这样的直线l有( )
=1的右焦点作直线l交双曲线于A、B两点,若│AB │=4,则这样的直线l有( )
A.1条 B.2条 C.3条 D.4条
14.某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁 盘,根据需要,软件至少买3片,磁盘至少买2盒,则不同的选购方式共有( )
A.5种 B.6种 C.7种 D.8种
二、填空题: (本大题共4小题,每小题4分,共16分)
15.已知a=│x+yi│(x,y∈R),无穷数列{an}各项和为1,则x2y4的最大值为 .
16.若方程![]() =1表示椭圆或双曲线,则其焦距等于 .
=1表示椭圆或双曲线,则其焦距等于 .
17.函数f(x)=lg(3x+1+9x-18)的值域是 .
18.给出下列命题:
(1){正四棱柱}∩{长方体}={正方体}
(2)函数y=x3既是奇函数又是增函数
(3)不等式x2-4ax+3a2<0的解集为{x│a<x<3a}
(4)函数y=f(x)的图像与直线x=a至多有一个交点
(5)A={x│f(x)=0,x∈R},B={x│g(x)=0,x∈R},C={x│f(x)·g(x)=0,x∈R},则 C=A∪B
其中正确命题的序号是 .
三、解答题:(本大题共6题,共74分,解答应写出文字说明,证明过程或演算步骤)
19.设复数z=a+bi(a,b∈R)存在实数t,使得![]() =
=![]() -3ati,如果│z-2 │≤a,求复数z的辐角主值的取值范围.
-3ati,如果│z-2 │≤a,求复数z的辐角主值的取值范围.
20.在△ABC中,三边a、b、c依次成等差数列,各边所对的角分别为A、B、C,求5cosA-4cos AcosC+5cosC的值.
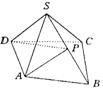
21.如图,已知四棱锥S—ABCD的侧面SCD⊥底面ABCD,BC∥AD,BC⊥SC,且SC=SD=CD=BC=2AD =2,P为SB的中点,求:(1)异面直线SD与BC的距离;(2)二面角A—SB—C的大小;(3)三棱锥 S—APD的体积.
22.某企业在“减员增效”中,对部分人员实行分流,规定分流人员第一年可以到原单位领 取工资的100%,从第二年起,以后每年只能在原单位按上一年的![]() 领取工资,该企业根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属 投资阶段,没有利润,第二年每人可获b元收入,从第三年起每人每年的收入可在上一年基 础上递增5%,如果某人分流前工资收入每年a元,分流后第n年总收入为an元.(1)求an;
(2)当b=
领取工资,该企业根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属 投资阶段,没有利润,第二年每人可获b元收入,从第三年起每人每年的收入可在上一年基 础上递增5%,如果某人分流前工资收入每年a元,分流后第n年总收入为an元.(1)求an;
(2)当b=![]() a时,这个人哪一年收入最少,最少收入是多少?(3)当b≥
a时,这个人哪一年收入最少,最少收入是多少?(3)当b≥![]() a时,是否一定可以保证这个人分流一年后的年收入永远超过分流前的年收入.
a时,是否一定可以保证这个人分流一年后的年收入永远超过分流前的年收入.
23.已知二次函数f(x)=ax2+bx+c(a,b∈R,a>0),设方程f(x)=x的两个实数根分别为x1 ,x2.
(1)如果x1<2<x2<4,设函数f(x)的对称轴为x=x0,求证:x0>-1.
(2)如果│x1│<2,│x2-x1│=2,求b的取值范围.
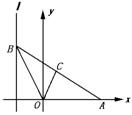
24.如图,给出定点A(a,0)(a>0)和直线l∶x=-1,B是直线l上的动 点,∠BOA的角平分线交AB于C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系 .

参考答案
【同步达纲练习】
一、DABCA ACDCD ACCC
二、15.![]() 16.2
16.2![]() 17.R 18. ②④
17.R 18. ②④
三、19.∵z=a+bi(a,b∈R),![]() =
=![]() +(
+(![]() -3at)i,∴a+bi=
-3at)i,∴a+bi=![]() -(
-(![]() -3at)i,∴
-3at)i,∴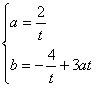 消去t,得b=6-2a①,由│z-2│≤a得(a-2)2+b2≤a2②,将①代入② 得a2-7a+10≤0,∴2≤a≤5.设argz=θ,则tgθ=
消去t,得b=6-2a①,由│z-2│≤a得(a-2)2+b2≤a2②,将①代入② 得a2-7a+10≤0,∴2≤a≤5.设argz=θ,则tgθ=![]() =
=![]() =
=![]() -2.∵-
-2.∵-![]() ≤
≤![]() -2≤1
-2≤1
∴0≤θ≤![]()
或2π-arctg![]() ≤θ<2π.
≤θ<2π.
20.由题意得2b=a+c,即2sinB=sinA+sinC,即2sin(A+C)=sinA+sinC,∴4sin![]() cos
cos![]() =2sin
=2sin![]() cos
cos![]() .∵sin
.∵sin![]() ≠0,∴cos
≠0,∴cos![]() =2sin
=2sin![]() .∴5cosA-4cosAcosC+5cosC=5×2 cos
.∴5cosA-4cosAcosC+5cosC=5×2 cos![]() cos
cos![]() -4×
-4×![]() 〔cos(A+C)+cos(A-C)〕=2c os2
〔cos(A+C)+cos(A-C)〕=2c os2![]() -2〔2cos2
-2〔2cos2![]() -1+2×4(1-cos2
-1+2×4(1-cos2![]() )-1〕=4.
)-1〕=4.
21.(1)作SE⊥DC于E.∵平面SCD⊥平面ABCD,∴SE⊥平面ABCD.∴SE⊥BC.又BC⊥SC,∴BC⊥ 平面SCD,∴C到SD的距离即为SD和BC的距离.∵△SDC为正三角形,∴所求异面直线的距离为 2×![]() =
=![]() .
.
(2)易知AS=AB=![]() ,而P为SB的中点,∴AP⊥BS,连PC,∵SC=BC=2,∴PC⊥SB.∴
∠APC即为二面角A—SB—C的平面角,在Rt△SEB中,得SB=
,而P为SB的中点,∴AP⊥BS,连PC,∵SC=BC=2,∴PC⊥SB.∴
∠APC即为二面角A—SB—C的平面角,在Rt△SEB中,得SB=![]() =2
=2![]() ,∴AP=
,∴AP=![]() =
=![]() .在Rt△ADC中,AC=
.在Rt△ADC中,AC=![]() =
=![]() .在Rt△SCB中,PC=
.在Rt△SCB中,PC=![]() ×2=
×2=![]() . ∵AP2+PC2=AC2,∴∠APC=
. ∵AP2+PC2=AC2,∴∠APC=![]() ,即所求二面角为
,即所求二面角为![]() .
.
(3)VS-APD=VP-SAD.∵BC∥AD,P为SB中点,设d1为B到平面SAD的距离,∴V P-SAD=![]() VB-SAD=
VB-SAD=![]() ·
·![]() ·
·
S△SAD·d1,而d1=![]() .∴VS-APD=
.∴VS-APD=![]() ·
·![]() ·AD·SD·
·AD·SD·![]() ×2=
×2=![]() .
.
22.(1)根据题意知,当n=1时,an=a.
当n≥2时,an=a(![]() )n-1+b(1+
)n-1+b(1+![]() )n-2=a(
)n-2=a(![]() )n-1+b(
)n-1+b(![]() )n-2.
)n-2.
∴an=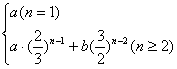
(2)由已知b=![]() a,当n≥2时,an=a(
a,当n≥2时,an=a(![]() )n-1+
)n-1+![]() a(
a(![]() )n-2≥2
)n-2≥2![]() =
=![]() a,要使上式等号成立 ,当且仅当a(
a,要使上式等号成立 ,当且仅当a(![]() )n-1=
)n-1=![]() a(
a(![]() )n-2即 (
)n-2即 (![]() )2n-2=(
)2n-2=(![]() )4解得n=3.因此这个人第3年收入 最少,最少收入为
)4解得n=3.因此这个人第3年收入 最少,最少收入为![]() a.
a.
(3)当n≥2时,an=a(![]() )n-1+b(
)n-1+b(![]() )n-2≥a(
)n-2≥a(![]() )n-1+(
)n-1+(![]() )a·(
)a·(![]() )n-2≥2
)n-2≥2![]()
=a. 上式等号成立,需b=![]() a且(
a且(![]() )n-1=
)n-1=![]() (
(![]() )n-1,即n=1+log
)n-1,即n=1+log![]()
![]() .虽然1+log
.虽然1+log![]()
![]() >1+log
>1+log![]()
![]() =2,但1+log
=2,但1+log![]()
![]() 不是自然数,因此等号不可能取到,即当n>2时,有an>a,但n=2时,a2=
不是自然数,因此等号不可能取到,即当n>2时,有an>a,但n=2时,a2=![]() a+
a+![]() a=
a=![]() a>a.综上知,当b≥
a>a.综上知,当b≥![]() a 时,一定可以保证这个人分流一年后的年收入永远超过分流前的年收入.
a 时,一定可以保证这个人分流一年后的年收入永远超过分流前的年收入.
23.令(1)g(x)=ax2+(b-1)x+1=0,由题意得
![]()
![]()
![]() -4a+2b<0
-4a+2b<0![]()
![]() <1,∴ x0=-
<1,∴ x0=-![]() >-1.
>-1.
(2)对于ax2+(b-1)x+1=0,令b-1=c,则ax2+cx+1=0.由│x2-x1│=2![]()
![]() =2即c2=4a2+4a①,又│x1│<2,∴-6<x 1+x2<6
=2即c2=4a2+4a①,又│x1│<2,∴-6<x 1+x2<6![]() -6<-
-6<-![]() <6
<6![]() c2<36a2.又Δ>0
c2<36a2.又Δ>0![]() c2-4a>0,∴4 a<c2<36a2②.由①、②得a>
c2-4a>0,∴4 a<c2<36a2②.由①、②得a>![]() ,∴c2=4a2+4a>
,∴c2=4a2+4a>![]() ,∴c>
,∴c>![]() 或c<-
或c<-![]() ,∴b>
,∴b>![]() 或b<
或b<![]() .
.
24. 解法一 依题意,记B(-1,b)(b∈R),则直线OA和OB的方程分别为y=0和y=-bx.
设点C(x,y),则有0≤x≤a,则OC平分∠AOB,知点C到OA、OB距离相等,根据点到直线的距 离公式得
|y|=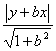
![]()
依题设,点C在直线AB上,故有
y=-![]() (x-a)
(x-a)
由x-a≠0得b=-![]() ②
②
将②代入①式得
y2[1+![]() ]=[y+
]=[y+![]() ]2
]2
整理得 y2[1-ax2-2ax+(1+a)y2]=0
若y≠0,则(1-a)x2-2ax+(1+a)y2=0 (0<x<a);
若y=0,则b=0,∠AOB=π,点C的坐标为(0,0),满足上式,
综上得点C的轨迹方程为
(1-a)x2-2ax+(1+a)y2=0(0≤x<a)
(Ⅰ)当a=1时,轨迹方程化为y2=x(0≤x<1) ③
此时,方程③表示抛物线弧段;
(Ⅱ)当a≠1时,轨迹方程化为
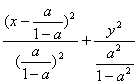 =1(0≤x<a). ④
=1(0≤x<a). ④
所以,当0<a<1时,方程④表示椭圆弧段;
当a>1时,方程④表示双曲线一支的弧段.
解法二 如图,设D是l与x轴的交点,过点C作CE⊥x轴,E是垂足.
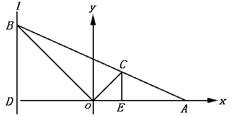
(1)当|BD|≠0时,设点C(x,y),则0<x<a,y≠0
由CE∥BD得
|BD|=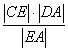 =
=![]() (1+a)
(1+a)
∠COA=∠COB=∠COD-∠BOD
=π-∠COA-∠BOD
2∠COA=π-∠BOD
tg(2∠COA)=![]() ,tg(π-∠BOD)=-tg∠BOD
,tg(π-∠BOD)=-tg∠BOD
tg∠COA=![]() ,tg∠BOD=
,tg∠BOD=![]() =
=![]() (1+a)
(1+a)
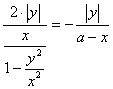 (1+a)
(1+a)
整理得 (1-a)x2-2ax+(1+a)y2=0 (0<x<a).
(Ⅲ)当|BD|=0时,∠BOA=π,则点C的坐标为(0,0),满足上式
综合(Ⅰ)、(Ⅱ),得点C的轨迹方程为
(1-a)x2-2ax+(1+a)y2=0(0≤x<a).
以下同解法一.
