| 班级 | 姓名 | 学号 | 时间 | |||||||
| 课题 | 直线与平面的垂直 | 设计 | ||||||||
| 一、方法点击 1、 掌握直线与平面垂直的定义、判定与性质,并能运用这些知识进行论证和解题。 2、 完整正确的掌握直线与平面所成角的概念,其中求斜线与平面所成角时常采用射影转化法。 3、 证明垂直问题,常通过“线线垂直”与“线面垂直”之间的转化来实现。 二、知能达标 1、给出下列命题:(1)a∥b,a⊥ A (1) (2) B (1) (2) (3) C (2) (3) (4) D (1) (2) (4) 2、如果平面 A l⊥ 3、一条直线与平面所成的角为 A 4、给出下列命题:(1)直线l和平面 5、长方体的一条体对角线与其一端点出发的三个面所成角分别为 6、∠BAC=90°, ∠ 7、如图,ABCD是矩形,AB=a,BC=b(a>b),沿对角线AC把△ADC折起,使AD⊥BC, (1)求证BD是异面直线AD与BC的公垂线,(2)求BD的长。 D
D C C A B A B
| ||||||||||
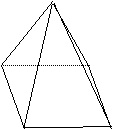
| 8、如图,在四棱锥P—ABCD中,侧面PCD是边长等于2cm的等边三角形,底面ABCD是面积为
B A
C D **8、如图,正方体ABCD-A 1B 1C 1D1中,EF是异面直线AC和A 1D的公垂线,求证:EF∥BD1
A1 B1
E
D C F A B
|
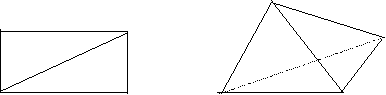
 P
P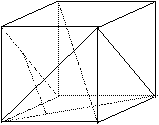 D1 C1
D1 C1