直线与平面的平行和垂直

高考能力测试步步高数学基础训练32

基础训练32　直线与平面的平行和垂直

●训练指要

理解直线与平面的位置关系及其特征，熟练地判断(证明)直线与平面平行和垂直.

一、选择题

1.如果平面外的一条直线上有两个点到这个平面的距离相等，则这条直线和平面的

位置关系是

A.平行  　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.相交

C.平行或相交　　　　　　　　　　　　　　　　　　　　　　　　 D.以上都不对

2.下列命题中错误的是

A.若一直线垂直于一个平面，则此直线垂直于这个平面内的所有直线

B.a、b是异面直线，过a有且只有一个平面与b平行

C.平面外的直线垂直于这平面的一条垂线，则此直线平行于这个平面

D.一条直线垂直于一条斜线在一个平面内的射影，则这条直线垂直于这条斜线

3.(2003年上海春招)关于直线a、b、l以及平面M、N，下列命题中正确的是

A.若a∥M,b∥M,则a∥b

B.若a∥M,b⊥a,则b⊥M

C.若aM,bM,且l⊥a,l⊥b,则l⊥M

D.若a⊥M,a∥N,则M⊥N

二、填空题

4.过直角三角形斜边中点做垂直于它所在的平面的直线，则过这条直线上任一点和直角三角形各顶点所连结的斜线段的长、短关系是_________；这三条斜线段和这个平面所成的角的大小关系是_________.

5.直角AOB的边OA∥平面α，∠AOB在平面α内的射影仍为直角，则边OB所在直线与α的关系为_________.

三、解答题

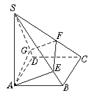6.点A、B、C、D不共面，点M、N分别为△ABD、△CBD的重心.求证：MN∥平面ACD.

7.如图，ABCD为正方形，SA⊥平面ABCD，过A且垂直于SC的平面分别交SB、SC、SD于E、F、G.求证：AE⊥SB、AG⊥SD.

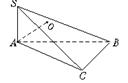8.如图，△ABC是锐角三角形，SA⊥平面ABC，连结SB和SC，得到△SBC，过A作AO⊥平面SBC，其中O为垂足，求证：O不是△SBC的垂心.

高考能力测试步步高数学基础训练32答案

一、1.C　2.D  3.D

二、4.相等　相等　5.平行或斜交

三、6.△的重心将中线分成2∶1的两段即可证

7.略

8.反证法