高考第一轮复习单元测试（六）
直线与圆锥曲线
一、选择题（每小题5分，共60分）
1.如果
三点在同一条直线上，那么
的值是
A.-6 B.-7 C.-8 D.-9
2．有5辆6吨的汽车和4辆4吨的汽车，要运送最多货物，完成这项运输任务的线性目标函数是
A．
B．
C．
D．
3.曲线
与曲线
一定有
A.相等的长轴 B.相等的焦距 C.相等的离心率 D.相同的准线
4.将直线
绕着它与
轴的交点逆时针旋转
的角后，在
轴上的截距是
A.
B. 
C. 
D.
5．在同一坐标系中，方程
的曲线大致是
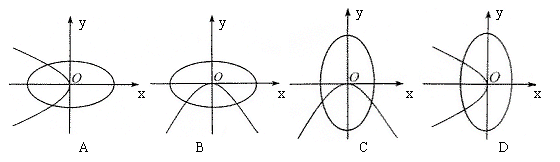
6.双曲线的渐近线为
,且过点
,则此双曲线的共轭双曲线的方程为
A.
B.
C.
D.
7．已知直线
相切，则三条边长分别为
的三角形
A．是锐角三角形 B．是直角三角形 C．是钝角三角形 D．不存在
8.一动圆圆心在抛物线
上,且动圆恒与直线
相切,则动圆必过定点
A.
B.
C.
D.
翰林汇9.已知
,直线
：
，直线
：
，与的位置关系是
A．平行 B．垂直 C．重合 D．相交但不垂直
10．椭圆
的两个焦点
三等分它的两条准线间的距离，那么它的离心率是
A．
B．
C．
D．
11.已知抛物线
的焦点弦
的两端点为
,
,则式子
的值一定等于
A．
B．
C．
D．
12．已知双曲线中心在原点且一个焦点为
直线
与其相交于M、N两点，
MN中点的横坐标为
则此双曲线的方程是
A．
B．
C．
D．
二、填空题（每小题4分，共16分）
13.抛物线的顶点在原点，对称轴是坐标轴，且焦点在直线
上，则此抛物线方程为__________________.
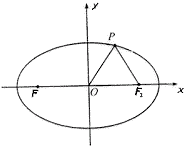
14. 如图，F1，F2分别为椭圆的左、右焦点，
点P在椭圆上，△POF2是面积为
的正三角形，则
的值是
.
15.若直线
沿轴负方向平移3个单位，再沿轴正方向平移一个单位后，又回到原来的位置，那么直线的斜率为
.
16.给出问题：F1、F2是双曲线
=1的焦点，点P在双曲线上.若点P到焦点F1的距
离等于9，求点P到焦点F2的距离.某学生的解答如下：
双曲线的实轴长为8，由PF1－PF2=8，即9－PF2=8，得PF2=1或17.
该学生的解答是否正确？若正确，请将他的解题依据填在下面空格内，若不正确，将正确
的结果填在下面空格内.
_____________________________________________________________________________.
三、解答题（共74分）
17.（本小题满分12分）已知椭圆的焦点为
和
，直线
是椭圆的一条准线.
（1）求椭圆的方程；
（2）又设
在此椭圆上，且
，求
的值.
18．（本小题满分12分）已知圆
，
（1）若
为圆上任一点，
，求
的最大值和最小值；
（2）求
的最大值和最小值；
（3）求
的最大值.
19．（本小题满分12分）已知点
、
，
为坐标原点.
（1）若点
在线段
上，且
，求
的面积；
（2）若原点关于直线的对称点为
，延长
到，且
.已知直线：
经过点，求直线的倾斜角.
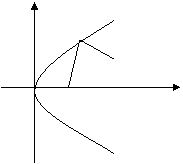20．（本小题满分12分）如图，
为抛物线
的焦点，
为抛物线内一定点，为抛物线上一动点，且
的最小值为8.
（1）求该抛物线方程； P
（2）如果过的直线交抛物线于、
两点，
A
且
，求直线倾斜角的取值范围.
O F
21．（本题满分14分）本题共有2个小题，第1小题
满分5分，第2小题满分7分.
|
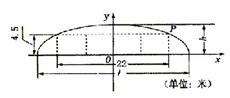
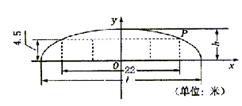
求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状.
（1）若最大拱高
为6米，则隧道设计的拱
宽是多少？
（2）若最大拱高不小于6米，则应如何设
计拱高和拱宽，才能使半个椭圆形隧道的
土方工程量最最小？
（半个椭圆的面积公式为
，柱体体积为：底面积乘以高.）
22．（本题满分14分）本题共有3个小题，第1小题满分4分，第2小题满分4分，第
3小题满分6分.
在以为原点的直角坐标系中，点
为
的直角顶点.已知
，且
点
的纵坐标大于零.
（1）求向量
的坐标；
（2）求圆
关于直线对称的圆的方程；
（3）是否存在实数
，使抛物线
上总有关于直线对称的两个点？若不存
在，说明理由：若存在，求的取值范围.
高考第一轮复习单元测试（六）
直线与圆锥曲线参考答案
一、选择题（每小题5分，共60分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | B | B | B | A | B | B | D | B | B | B | D |
二、填空题（每小题4分，共16分）
13．
或
14．
15．
16．
三、解答题（74分）
17．（1）
；
（2）
。
18．（1）
，
；（2）
，
；（3）
19．（1）解：设
，则
，因为，故
；
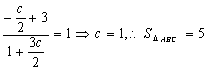（2）
20.（1）解：设点到抛物线的准线：
的距离为
，由抛物线的定义知
，（1分）
（3分）
抛物线的方程为
.（4分）
（2）解法一：由（1）得
，设直线的方程为
，显然，
把直线方程代入抛物线，得
，
即
,(10分)
直线斜率的取值范围为
,
所以，直线倾斜角的取值范围为
.(12分)
21．[解]（1）如图建立直角坐标系，则点P（11，4.5）， 椭圆方程为.
|
.因此隧道的拱宽约为33.3米.
（2）[解一]
由椭圆方程，得
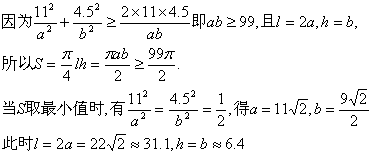
故当拱高约为6.4米、拱宽约为31.1米时，土方工程量最小.
[解二]由椭圆方程，得 于是
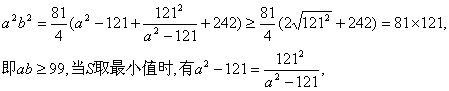
得
以下同解一.
22．[解]（1）
设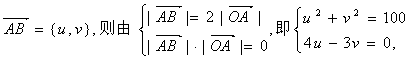
得
所以v－3>0,得v=8,故={6，8}.
（2）由
={10，5}，得B（10，5），于是直线OB方程：
由条件可知圆的标准方程为：(x－3)2+y(y+1)2=10,
得圆心（3，－1），半径为
.设圆心（3，－1）关于直线OB的对称点为（x ,y）则
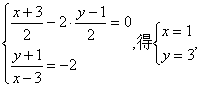故所求圆的方程为(x－1)2+(y－3)2=10.
（3）设P (x1,y1), Q (x2,y2) 为抛物线上关于直线OB对称两点，则
故当
时，抛物线y=ax2－1上总有关于直线OB对称的两点.