一道练习题的多种解法
———直线与圆锥曲线的位置关系
临沂现代试验学校高中部 恨水无情
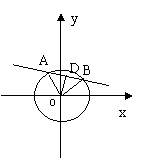
题目:直线l:y=ax+b与曲线x2+y2=1相交于A,B两点.若AO⊥BO
(O为坐标原点,).求实数a,b满足什么关系?
解法(1):复数法
设ZOA=cosθ+isinθ, AO⊥BO,则ZOB=
=sinθ-i cosθ
∴A(cosθ,sinθ),B(sinθ, cosθ)
∴lAB=
=
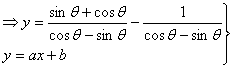
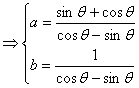
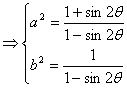
∴a2+1=
=
=2b2
∴实数a,b的关系是a2+1=2b2.
本解法是笔者抄了资料上的解法,甚觉有点麻烦,所以就写了此文.
解法(2):参数法1
设圆x2+y2=1的参数方程
∴设点B(cosθ,sinθ), AO⊥BO,则点A(cos(θ+
),sin(θ+))
即点A(-sinθ, cosθ).又因为点A,B是直线l:y=ax+b与圆的交点
∴
,
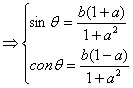且sin2θ+ cos2θ=1⇒a2+1=2b2.
∴实数a,b的关系是a2+1=2b2.
解法(3):参数法2
设圆x2+y2=1的参数方程
∴设点B(cosθ,sinθ), AO⊥BO,则点A(cos(θ+),sin(θ+))
即点A(-sinθ, cosθ).又因为点A,B是直线l:y=ax+b与圆的交点
⇒
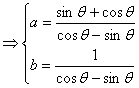
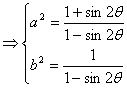
∴a2+1===2b2
∴实数a,b的关系是a2+1=2b2.
解法(4)参数法3
设直线的参数方程
则A(
),B(
)
将参数方程中的x,y代入圆的方程
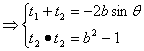
有AB=
,
即 
化简得
解法(4):整体法1
∵AO⊥BO,过点O作l的垂线OD,垂足为D,
则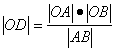
,
且
,代入上式
,所以原点O到直线l: y=ax+b的距
离为d=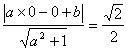
⇒a2+1=2b2.
∴实数a,b的关系是a2+1=2b2.
解法(5)整体法2
有已知AO⊥BO,,设直线l与曲线的交点A(x1,y1),B(x2,y2)
则
=
(*)
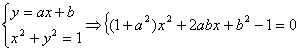
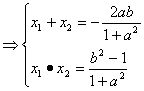代入(*)式,得
=
⇒a2+1=2b2.
∴实数a,b的关系是a2+1=2b2.
解法(6)向量法1
由解法(4,)
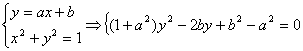
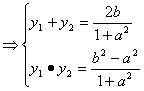
设向量
⇒
⇒a2+1=2b2.
∴实数ab的关系是a2+1=2b2.
解法(7)向量法2
由解法(5)
x12+y12+x22+y22=(y2-y1)2+(x2-x1)2
⇒a2+1=2b2.
∴实数a,b的关系是a2+1=2b2.
练习:
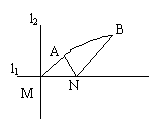1.(98年全国)如图:直线l1,l2相交于点M, l1⊥l2 ,点N∊l1,以A,B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若ΔAMN为锐角三角形,
,建立适当的坐标系,求曲线段C的方程.
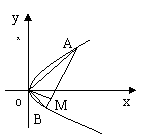2.(00年京皖春)如图:设点A,B为抛物线y2=4px(p>0)上原点以外的两个动点.已知OA⊥OB,OM⊥AB,求点M的轨迹方程,并说明它表示什么曲线.