| 班级 | 姓名 | 学号 | 时间 | |||||||
| 课题 | 圆柱、圆锥、圆台、球的有关概念及性质 | 设计 | ||||||||
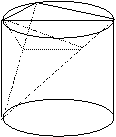
| 一、方法点击: 1、 圆柱、圆锥、圆台、球中的点、线、面之间的位置关系及数量关系是解决此类几何体问题的基础,必须熟练掌握。 2、 了解旋转体的形成,轴截面的几何特征及其在解题中的应用,轴截面为旋转体的特征多边形,其中的量反映了 几何体的特征,解题时不可忽视轴截面的应用。 3、 圆台的有关问题常化为圆锥来解决, 4、 球面距离的问题需紧扣定义,努力寻找这两点关于球心的张角。球与其它几何体的结合体的问题,则需紧抓公共点。 二、知能达标: 1、下列命题:(1)过直线外一点作直线的垂线只有一条;(2)过空间一点作已知平面的垂线只有一条;(3)圆锥的轴截面是直角三角形,则它的侧面展开扇形的中心角为 A (1) (2) (3) B (1) (3) (4) C (1) (2) (4) D (2) (3) (4) 2、两个圆锥的母线长相等,它们的侧面展开图恰好拼成一个圆,它们的侧面积之比为1:2,则它们的高之比为 ( D ) A 1:1 B 1:2 C 3、一个圆台的上、下底面积分别为 A 5cm B 10cm C 15cm D 20cm 4、在等边圆柱O 1O2中,长度为1的两底面半径O 1A 1 ,O 2A2互相垂直,则 ( B ) A A 1A2与底面所成角的正切值为2 B A 1A2与O 1O2成角的正切值为 C O 1A 1与O 2A2间距离为1 D A 1A2与O 1O2间距离为 5、圆柱轴截面是边长为10的正方形ABCD,从A点出发,沿圆柱侧面到C点的最短距离为 。 6、一个正方体内接于高为40cm,底面半径为30cm的圆锥,则正方体的棱长为 。 7、球面上有三点,其中任意两点的球面距离都等于大圆周长的1/6,经过这三点的小圆周长为 8、高为8cm,底面半径为4cm的圆柱内有一长10cm的线段,线段两端点各在一个底面的圆周上,求:(1)这条线段与底面所成的角;
OO
| ||||||||||
|
9、设圆锥的底面半径和高分别为r,h,若圆锥的体积等于它的内切球体积的2倍, 求证: ☆ 试一试:已知AB为圆柱底面上的直径,C为底面圆周上的一点,AA‘为一条母线,如果AB=2,BAC=60°,二面角A—A’B—C为60°,求点A到平面A’BC的距离d。 C
A B O D A’ |
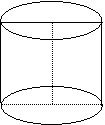 (2)该线段与圆柱轴之间的距离。
(2)该线段与圆柱轴之间的距离。