双曲线标准方程及几何性质

高考能力测试步步高数学基础训练27

基础训练27　双曲线标准方程及几何性质

●训练指要

熟练掌握双曲线的定义、标准方程及几何性质；能优先考虑定义、简化运算；会用待定系数法求双曲线方程.

一、选择题

1.(2002年全国高考题)设θ∈(0,)，则二次曲线x²cotθ-y²tanθ=1的离心率的取值范围为

A.(0，)　　　　　　　　　　　　　　　　　　　　　　　 B.()

C.()　　　　　　　　　　　　　　　　　　　　　　D.(，+∞)

2.若双曲线的两条渐近线是y＝±x，焦点F₁(－，0)、F₂(，0)，那么它的

两条准线间的距离是

A.　　　　　　　　　　　　　　　　　　　　　　　　B.

C.　　　　　　　　　　　　　　　　　　　　　　　　D.

3.如果方程表示双曲线，则k的取值范围是

A.k＞2　　　　　　　　　　　　　　　　　　　　　　　　　 B.k＜2

C.k＞5或k＜2　　　　　　　　　　　　　　　　　　　　D.2＜k＜5或k＜－2

二、填空题

4.已知双曲线渐近线方程为y＝±x，且焦点都在圆x²＋y²＝100上，则双曲线方程为_________.

5.设F₁、F₂是双曲线 (a＞0)的两个焦点，P在双曲线上，∠F₁PF₂＝90°，若Rt△F₁PF₂的面积是1，则a的值是_________.

三、解答题

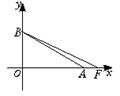
6.如图，OA是双曲线的实半轴，OB是虚半轴，F为焦点，且∠BAO＝30°，S_△ABF＝，求该双曲线的方程.

7.在双曲线的一支上有不同三点A(x₁，y₁)、B(x₂，6)、C(x₃，y₃)与点F(0，5)的距离AF、BF、CF依次成等差数列，

(1)求y₁＋y₂的值；

(2)求证线段AC的垂直平分线经过一定点，求出定点的坐标.

8.(2002年全国高考题)设点P到点M(-1，0)、N(1，0)距离之差为2m，到x轴、y轴距离之比为2.求m的取值范围.

高考能力测试步步高数学基础训练27答案

一、1.D　2.A  3.D

二、4.　5.1

三、6.

7.(1)12　(2)(0,)

提示：(1)F(0，5)为椭圆上焦点，化成方程为y=，设双曲线离心率为e，则AF=e(y₁－

∵2BF=AF+CF,

∴y₁+y₂=12.

(2)设AC的中点为M(x₀,y₀),则y₀==6.即M(x₀,6).

又A、C在双曲线上，

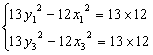∴两式相减，得12(x₁²－x₃²)=13(y₁²－y₃²)

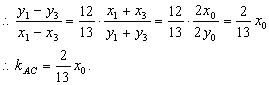
故AC的垂直平分线方程是y－6=－

令x=0得y=,故它经过定点(0，).

即AC垂直平分线经过定点(0，).

8.(－,0)∪(0, )

提示：设P(x,y)，依题设得,即y=±2x,x≠0.　　　　　　　　  ①

因此，点P(x,y)、M(－1,0)、N(1，0)三点不共线，得

PM－PN＜MN=2

∵PM－PN=2m＞0,

∴0＜m＜1.

因此，点P在以M、N为焦点，实轴长为2m的双曲线上，故　　　②

将①式代入②式，并解得

x²=.

∴1－m²＞0,

∴1－5m²＞00＜m＜.

(－,0)∪(0, )