双曲线的几何性质

高三双曲线的几何性质

1. 已知双曲线的左右焦点分别为F₁、F₂，左准线为L，能否在双曲线的左支上求一点P，使PF₁是P到L的距离d与PF₂的等比中项？若能，求出P点坐标，若不能，说明理由。

解：假定在左支上存在一点P适合题意,

则有,

∴,又PF₂－PF₁ = 10,

∴,

∴ ,

又由于PF₁＋PF₂≥F₁F₂ = 26,上两式矛盾,

∴P不存在.翰林汇

2.一双曲线以y轴为右准线,其右支过点M(1,2),且它的虚轴长、实轴长、焦距顺次成等差数列,试求：

(1)双曲线右焦点F的轨迹方程;(2)实轴最长的双曲线方程;

(3)过点M、F的弦的另一端点N的轨迹方程(不必求出轨迹范围).

解：(1)(x-1)²+(y-2)²=(x>0);

(2)9(x+4)²-16(y-2)²=225;

(3)9x²-16y²+82x+64y-55=0.翰林汇翰林汇

3.点P在双曲线=1上,F₁、F₂是左右焦点,O为原点,

求 的取值范围.

解： 设点P(x₀,y₀)在右支上,离心率为e,

则有PF₁=ex₀＋a,PF₂=ex₀－a,OP==1,

所以,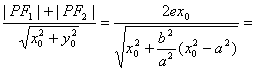

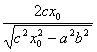设t=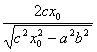, ∴t²=,解得

这里t²－4＞0,又≥a²,

∴≥a²　 ∴≥1 ∴≥0,由此得：

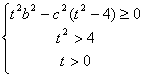解得2＜t≤2e

当点P在左支上时,同理可以得出此结论.翰林汇翰林汇

翰林汇4.已知直线y=x+b与双曲线2x²－y²=2相交于A, B两点, 若以AB为直径的圆过原点,

求b的值翰林汇。翰林汇

解：翰林汇　设A(x₁,y₁), B(x₂,y₂), 则 由条件可得：

x₁+x₂=2b, x₁x₂=－b²－2, y₁y₂=－x₁x₂,

最后得b=±2.翰林汇

翰林汇5.已知双曲线的中心在原点,对称轴为坐标轴,离心率,一条准线的方程为,求此双曲线的标准方程.

解： 由题设, 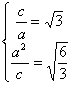 解得 .

∴双曲线方程为 .翰林汇

6.已知点F与直线l分别是双曲线x²－3y²=3的右焦点与右准线, 以F为左焦点 , l为左准线的椭圆C的中心为M, 又M关于直线y=2x的对称点M^′恰好在已知双曲线的左准线上(如图),

求椭圆C的方程及其离心率.　　　　　　　　 

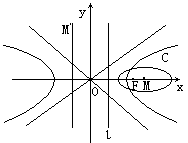
解：∵ F(2,0) , 再设P(x,y)在C上,

则由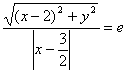, 得(1－e²)x²+y²+(3e²－4)x+4－e²=0,

于是中心为

由条件得方程为x²+2y²－5x+=0,

 即4x²+8y²－20x+23=0, 离心率

7.双曲线中点在原点，准线平行x轴，离心率为，若点P(0，5)到双曲线上的点的距离的最小值是2时，求双曲线的方程.翰林汇

翰林汇解几解解：设双曲线方程；M(x，y)为双曲线上任意一点.

由，∴，∴b²=c²－a²=.

而PM²=x²＋(y－5)²=(y－4)²＋5－a².

以下分a≤4或a＞4讨论，

得双曲线方程

8.已知P为双曲线3x²－5y²=15上的一点, F₁,F₂为其两个焦点, 且,求∠F₁PF₂的大小.

解：令∠F₁PF₂=θ, PF₁=m, PF₂=n, 则由余弦定理可得,

又由S_△=,

于是, 最后得.翰林汇

9.求双曲线的以点P(a,1)为中点的弦所在直线方程,并讨论a取怎样的值时这样的弦才存在.

解：y=ax－a²＋1.只有当－＜a＜或a＞或a＜－时,

以点P为中点的弦才存在.翰林汇

10. 翰林汇0已知双曲线的离心率, 半虚轴长为2, 求双曲线方程.

解：∵ , 可令a=4k, c=5k, 则b²=c²－a²=9k²=4,

∴.于是,

故双曲线方程为.翰林汇