椭圆标准方程及几何性质

高考能力测试步步高数学基础训练26

基础训练26　椭圆标准方程及几何性质

●训练指要

熟练掌握椭圆的定义、标准方程、几何性质；会用待定系数法求椭圆方程.

一、选择题

1.椭圆中心在坐标原点，对称轴为坐标轴，离心率为0.6，长、短轴之和为36，则椭圆方程为

A.

B.

C.

D.

2.若方程x²＋ky²＝2，表示焦点在y轴上的椭圆，那么实数k的取值范围是

A.(0，＋∞)　　　　　　　　　　　　　　　　　　　　　　 B.(0，2)

C.(1，＋∞)　　　　　　　　　　　　　　　　　　　　　　 D.(0，1)

3.已知圆x²＋y²＝4，又Q(，0)，P为圆上任一点，则PQ的中垂线与OP之交点M轨迹为(O为原点)

A.直线　　　　　　　　　　　　 B.圆　　　　　　　　　　　C.椭圆　　　　　　　　　D.双曲线

二、填空题

4.设椭圆的两个焦点为F₁、F₂，P为椭圆上一点，且PF₁⊥PF₂，则PF₁－PF₂＝_________.

5.(2002年全国高考题)椭圆5x²+ky²=5的一个焦点是(0，2)，那么k=_________.

三、解答题

6.椭圆=1(a＞b＞0),B(0,b)、B′(0,-b),A(a,0),F为椭圆的右焦点，若直线AB⊥

B′F,求椭圆的离心率.

7.在面积为1的△PMN中，tanM=,tanN=-2，建立适当的坐标系，求以M、N为焦点且过点P的椭圆方程.

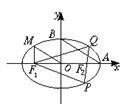
8.如图，从椭圆＝1(a＞b＞0)上一点M向x轴作垂线，恰好通过椭圆的左焦点F₁，且它的长轴端点A及短轴的端点B的连线AB∥OM.

(1)求椭圆的离心率e；

(2)设Q是椭圆上任意一点，F₂是右焦点，求∠F₁QF₂的取值范围；

(3)设Q是椭圆上一点，当QF₂⊥AB时，延长QF₂与椭圆交于另一点P，若△F₁PQ的面积为20，求此时椭圆的方程.

高考能力测试步步高数学基础训练26答案

一、1.C　2.D  3.C

二、4.2

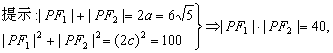
∴(PF₁－PF₂)²=100－2×40=20.

PF₁－PF₂=2.

5.1

三、6.

7.以MN所在直线为x轴，线段MN的中垂线为y轴建立坐标系，可得椭圆方程为

8.(1)　(2)［0,］　(3)

提示：(1)∵MF₁⊥x轴，

∴x_M=－c,代入椭圆方程求得y_M=,

∴k_OM=－

∵OM∥AB,

∴－

从而e=.

(2)设QF₁=r₁,QF₂=r₂,∠F₁QF₂=θ,则r₁+r₂=2a,F₁F₂=2c.

由余弦定理,得cosθ=

≥

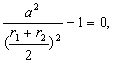
当且仅当r₁=r₂时，上式取等号.

∴0≤cosθ≤1,θ∈［0,］.

(3)椭圆方程可化为,又PQ⊥AB，

∴k_PQ=－

PQ:y=(x－c)代入椭圆方程，得5x²－8cx+2c²=0.

求得PQ=

F₁到PQ的距离为d=

∴

∴椭圆方程为