高 三 数 学(第23周)
椭圆的概念、性质,直线和椭圆的位置关系
【教学目标】
1、熟练掌握椭圆的定义:到两定点的距离之和等于定长(大于两定点间的距离)的点的集合及椭圆的第二定义,并能灵活地运用定义来解决有关问题。
2、熟练掌握中心在原点,焦点在坐标轴上的椭圆标准方程![]()
![]() 、
、![]() (a>b>0)及它们的顶点坐标、焦点坐标、准线方程和离心率、长轴长、短轴长、焦距焦半径的计算。
(a>b>0)及它们的顶点坐标、焦点坐标、准线方程和离心率、长轴长、短轴长、焦距焦半径的计算。
3、能运用图象法,判别式法来判断直线与椭圆的位置关系,结合一元二次方程根与系数的关系来讨论弦长、三角形面积、点到直线的距离等问题。
【知识讲解】
例1、已知椭圆的长轴长是短轴长的3倍,长、短轴都坐标上,且过点A(3,0),求椭圆的方程。
分析:椭圆的长、短轴都在坐标轴上,实质上就表示椭圆的中心在原点、焦点在坐标轴上,那么椭圆的方程一定是标准形式,但是由于不知道椭圆的焦点到底在x轴,还是在y轴上,因此要分两种情形来讨论。
解:1°若焦点在x轴上,设椭圆的方程为![]() ,把点A(3,0)代入得
,把点A(3,0)代入得
![]()
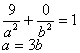 则a2=9,b2=1,所以所求椭圆方程为
则a2=9,b2=1,所以所求椭圆方程为![]() 。
。
2°若焦点在y轴上,设椭圆的方程为![]() 同理可得a2=81,b2=9,此时椭圆的方程为
同理可得a2=81,b2=9,此时椭圆的方程为![]() 。
。
说明:求出了焦点在x轴上的椭圆为![]() 后,不能简单地认为,焦点在y轴上的椭圆的方程就是
后,不能简单地认为,焦点在y轴上的椭圆的方程就是![]() 。因为椭圆过一定点(3,0),则求焦点在y轴上的椭圆仍应先设出方程,再用代入法求得。
。因为椭圆过一定点(3,0),则求焦点在y轴上的椭圆仍应先设出方程,再用代入法求得。
例2、已知椭圆![]() ,直线y=kx+4交椭圆于A、B两点,O为坐标原点,若kOA+kOB=2,求直线斜率k。
,直线y=kx+4交椭圆于A、B两点,O为坐标原点,若kOA+kOB=2,求直线斜率k。
解:解方程组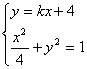 消去y,整理得(1+4k2)x2+32kx+60=0
消去y,整理得(1+4k2)x2+32kx+60=0
△=(32k)2-4×60(1+4k2)=16(4k2-15)>0 设A(x1,y1)、B(x2,y2)
kOA+kOB=2等价于![]() 即y1x2+y2x1=2x1x2
即y1x2+y2x1=2x1x2
即(kx1+4)x2+(kx2+4)x1=2x1x1 整理得(k-1)x1x2+2(x1+x2)=0
∵x1+x2=![]() x1x2=
x1x2=![]() ∴(k-1)
∴(k-1)![]() +2·
+2·![]() =0
=0
解之得 k=-15 满足△>0 ∴k=-15
例3、已知椭圆C的直角坐标方程为![]() ,若过椭圆C的右焦点F的直线
,若过椭圆C的右焦点F的直线![]() 与椭圆C相交于A (x1、y1),B (x2,y2),两点(其中y1>y2),且满足
与椭圆C相交于A (x1、y1),B (x2,y2),两点(其中y1>y2),且满足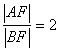 ,试求直线
,试求直线![]() 的方程。
的方程。
![]() 解:由已知条件,可知椭圆C的左焦点F的坐标为(1,0),设
解:由已知条件,可知椭圆C的左焦点F的坐标为(1,0),设![]() 的方程为y=k (x-1),则
的方程为y=k (x-1),则![]() 与C的两个焦点:A (x1、y1),B (x2,y2),y=k (x-1) ① ,①代入②得:
与C的两个焦点:A (x1、y1),B (x2,y2),y=k (x-1) ① ,①代入②得:
![]() ②
②
(3+4k2)x2-8k2x+4k2-12=0,x1+x2=![]() ③ x1·x2=
③ x1·x2=![]() ④,由条件
④,由条件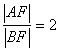
∴![]() ,即x1=3-2x2
⑤ ∴x2=
,即x1=3-2x2
⑤ ∴x2=![]() ,x1=
,x1=![]() ,代入④得:k2=
,代入④得:k2=![]() ,k=±
,k=±![]() ,易见x1<x2,因y1>y2,故k=
,易见x1<x2,因y1>y2,故k=![]() ∴
∴![]() 方程:y=-
方程:y=-![]()
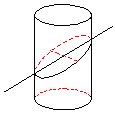 例4、底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,求这个椭圆的长、短轴长及离心率。
例4、底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,求这个椭圆的长、短轴长及离心率。
解:设椭圆的长半轴长为a,短半轴长为b,由题意可知,b=R=6,又因为截面与底面所成角等于30°,则![]() ,∴
,∴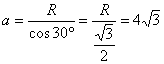 ,∴椭圆的长轴长为8
,∴椭圆的长轴长为8![]() ,短轴长为12,
,短轴长为12,![]() ,∴离心率
,∴离心率![]() 。
。
例5、设A(x1,y1)为椭圆x2+2y2=2上任意一点,过点A作一条直线![]() ,斜率为
,斜率为![]() ,又设d为原点到直线
,又设d为原点到直线![]() 的距离,r1、r2分别为点A到椭圆两焦点的距离。求证:
的距离,r1、r2分别为点A到椭圆两焦点的距离。求证:![]() 为定值。
为定值。
分析:根据椭圆的第二定义,即到定点的距离与到定直线的距离之比等于常数e(0<e<1)的点的轨迹是椭圆,椭圆![]() 上任一点P(x1,y1)到左焦点F1的距离PF1=a+ex1,到右焦点F2的距离PF2=a-ex1;同理椭圆
上任一点P(x1,y1)到左焦点F1的距离PF1=a+ex1,到右焦点F2的距离PF2=a-ex1;同理椭圆![]() 上任一点P(x1,y1)到两焦点的距离分别为a+ey1和a-ey1,这两个结论我们称之为焦半径计算公式,它们在椭圆中有着广泛的运用。
上任一点P(x1,y1)到两焦点的距离分别为a+ey1和a-ey1,这两个结论我们称之为焦半径计算公式,它们在椭圆中有着广泛的运用。
解:由椭圆方程![]() 可知a2=2,b2=1则c=1,∴离心率
可知a2=2,b2=1则c=1,∴离心率![]() ,由焦半径公式可知,
,由焦半径公式可知,![]() 。又直线
。又直线![]() 的方程为:
的方程为:
![]() 即x1x+2y1y-2=0,由点到直线的距离公式知,
即x1x+2y1y-2=0,由点到直线的距离公式知,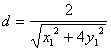 ,又点(x1,y1)在椭圆上,∴2y12=2=x12,∴
,又点(x1,y1)在椭圆上,∴2y12=2=x12,∴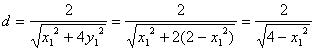 ,
,
∴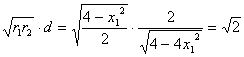 为定值。
为定值。
例6、已知椭圆![]() ,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1、F2距离的等比中项,若能找到,求出该点的坐标,若不能找到,请说明理由。
,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1、F2距离的等比中项,若能找到,求出该点的坐标,若不能找到,请说明理由。
解:假设存在满足条件的点,设M(x1,y1)a2=4,b2=3,∴a=2,![]() ,c=1,∴
,c=1,∴![]() ,
,![]() ,点M到椭圆左准线的距离
,点M到椭圆左准线的距离![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() ,这与x1∈[-2,0)相矛盾,∴满足条件的点M不存在。
,这与x1∈[-2,0)相矛盾,∴满足条件的点M不存在。
例7、直线![]() :6x-5y-28=0交椭圆
:6x-5y-28=0交椭圆![]() (a>b>2)于B、C两点,A(0,b)是椭圆的一个顶点,而△ABC的重心与椭圆的右焦点F重合,求椭圆的方程。
(a>b>2)于B、C两点,A(0,b)是椭圆的一个顶点,而△ABC的重心与椭圆的右焦点F重合,求椭圆的方程。
解:设BC的中点D(x0,y0),F(c,0),由定比分点公式可知![]() ,
,![]() ,∴
,∴![]() ,又点D在直线
,又点D在直线![]() 上,∴
上,∴![]() ①
①
![]() 又设B(x1,y1)、C(x2,y2)则
又设B(x1,y1)、C(x2,y2)则 ![]()
![]() 两式相减得:
两式相减得:
![]() ,
,![]()
![]() 代入得:
代入得:![]() ,∴2a2-5bc=0 ② 又a2=b2+c2
,∴2a2-5bc=0 ② 又a2=b2+c2
由①、②可得c=2或![]() 。
。
当c=2时,代入①得b=4,则a2=20,
当![]() 时,
时,![]() 舍去。
舍去。
∴所求椭圆的方程为![]() 。
。
例8、焦点在x轴上的椭圆![]() 绕上顶点逆时针旋转90°后,一条准线方程为y=
绕上顶点逆时针旋转90°后,一条准线方程为y=![]() ,求旋转前后的椭圆方程及它们的焦点坐标。
,求旋转前后的椭圆方程及它们的焦点坐标。
解:a=![]() ,b=3,c=
,b=3,c=![]() ,旋转后椭圆的中心为(3,3) ∴3+
,旋转后椭圆的中心为(3,3) ∴3+![]() =
=![]()
∴3+![]() =
=![]() 解之得:m=4或
解之得:m=4或![]() (均满足5m+5>9)
(均满足5m+5>9)
∴旋转前椭圆的方程为![]() 和
和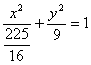 其焦点坐标分别为(-4,0)(4,0)和(-
其焦点坐标分别为(-4,0)(4,0)和(-![]() ,0)(
,0)(![]() ,0)
,0)
旋转后椭圆方程为![]() 和
和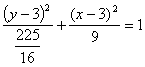
其焦点坐标分别为(3,7)(3,-1)和(3,![]() )、(3,
)、(3,![]() ).
).
例9、已知椭圆![]() (a>b>0)上两点A、B,直线
(a>b>0)上两点A、B,直线![]() 上有两点C、D,且ABCD是正方形。此正方形外接圆为x2+y2-2y-8=0,求椭圆方程和直线
上有两点C、D,且ABCD是正方形。此正方形外接圆为x2+y2-2y-8=0,求椭圆方程和直线![]() 的方程。
的方程。
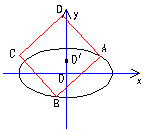 解:圆方程x2+y2-2y-8=0即x2+(y-1)2=9的圆心O'(0,1),半径r=3。
解:圆方程x2+y2-2y-8=0即x2+(y-1)2=9的圆心O'(0,1),半径r=3。
设正方形的边长为p,则![]() ,∴
,∴![]() ,又O'是正方形ABCD的中心,∴O'到直线y=x+k的距离应等于正方形边长p的一半即
,又O'是正方形ABCD的中心,∴O'到直线y=x+k的距离应等于正方形边长p的一半即![]() ,由点到直线的距离公式可知k=-2或k=4。
,由点到直线的距离公式可知k=-2或k=4。
![]() (1)设AB:y=x-2 由 y=x-2
(1)设AB:y=x-2 由 y=x-2
CD:y=x+4 x2+y2-2y-8=0
得A(3,1)B(0,-2),又点A、B在椭圆![]() 上,∴a2=12,b2=4,椭圆的方程为
上,∴a2=12,b2=4,椭圆的方程为![]() 。
。
(2)设AB:y=x+4,同理可得两交点的坐标分别为(0,4),(-3,1)代入椭圆方程得:![]() ,此时b2>a2(舍去)。
,此时b2>a2(舍去)。
综上所述,直线![]() 方程为y=x+4,椭圆方程为
方程为y=x+4,椭圆方程为![]() 。
。
例11、曲线2x2+y2=2a2(a>0)与连结A(-1,1),B(2,3)的线段没有公共点,求a的取值范围。
![]() 解:(1)若A、B在椭圆外部,则方程2x2+y2=2a2与直线AB的方程2x-3y+5=0组成的方程组无实数解,由
解:(1)若A、B在椭圆外部,则方程2x2+y2=2a2与直线AB的方程2x-3y+5=0组成的方程组无实数解,由 ![]() 消去y得
消去y得
![]()
22x2+20x+25-18a2=0无实数解,令
![]() 解得
解得![]() 。
。
(2)若A、B两点都在椭圆内部,显然交点B在椭圆上时是线段AB与椭圆有公共点的最大椭圆此时可解得![]() ,∴
,∴![]() 时,椭圆与线段AB无公共点,故所求a的取值范围是
时,椭圆与线段AB无公共点,故所求a的取值范围是![]() 或
或![]() 。
。
例12、AB是椭圆![]() (a>b>0)中不平行于对称轴的一条弦,M是AB的中点,O是椭圆的中心,求证:
(a>b>0)中不平行于对称轴的一条弦,M是AB的中点,O是椭圆的中心,求证:![]() 为定值。
为定值。
解:设A(x1,y1)B(x2,y2)∴![]() ,
,![]() ,
,
∴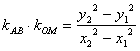 ,又点A、B在椭圆上,则:
,又点A、B在椭圆上,则:
![]()
∴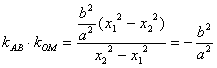 为定值。
为定值。
![]() 说明:若一条动直线与椭圆相交于两个点A、B,我们常常采用“设点法”设出点A(x1,y1),B(x2,y2)的坐标,然后把点的坐标代入椭圆的方程,
说明:若一条动直线与椭圆相交于两个点A、B,我们常常采用“设点法”设出点A(x1,y1),B(x2,y2)的坐标,然后把点的坐标代入椭圆的方程,![]() 两
两
![]()
式相减即可得到x1+x2,y1+y2及x1-x2,y1-y2的关系了,往往可以简化计算,达到很理想的效果,这种“设而不求”的解题思想在解析几何中有着广泛的应用,我们在学习时要充分注意。
例13、已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与该椭圆相交于P和Q,且OP⊥OQ,PQ=![]() ,求椭圆的方程。
,求椭圆的方程。
解:设所求椭圆方程为![]() ,依题知点P、Q的坐标满足方程组
,依题知点P、Q的坐标满足方程组![]() ① ∴ (a2+b2)x2+2a2x+a2 (1-b2)=0 ③,设③的两个根分别为x1、x2,则
① ∴ (a2+b2)x2+2a2x+a2 (1-b2)=0 ③,设③的两个根分别为x1、x2,则
![]() y=x+1 ②
y=x+1 ②
P (x1,x1+1)、Q (x2,x2+1) ∵OP⊥OQ,PQ=![]()
![]()
![]()
![]()
![]() ∴
∴![]() x1x2=-
x1x2=-![]() ∴
∴ ![]()
![]()
或 或
x1+x2=-![]() x1+x2=-
x1+x2=-![]()
![]()
![]()
![]()
![]() ∴ a2=2 a2=
∴ a2=2 a2=![]()
或 故所求椭圆的方程为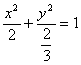 或
或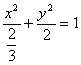
b2=![]() b2=2,
b2=2,
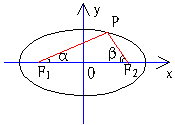
例14、已知椭圆![]() (a>b>0),P为椭圆上除长轴端点外的任一点,F1、F2为椭圆的两个焦点,(1)若
(a>b>0),P为椭圆上除长轴端点外的任一点,F1、F2为椭圆的两个焦点,(1)若![]() ,
,![]() ,求证:离心率
,求证:离心率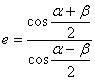 ;(2)若
;(2)若![]() ,求证:
,求证:![]() 的面积为
的面积为![]() 。
。
 分析:
分析:![]() 的两个顶点为焦点,另一点是椭圆上的动点,因此
的两个顶点为焦点,另一点是椭圆上的动点,因此![]() ,F1F2=2c,所以我们应以
,F1F2=2c,所以我们应以![]() 为突破口,在该三角形中用正弦定理或余弦定理,结合椭圆的定义即可证得。
为突破口,在该三角形中用正弦定理或余弦定理,结合椭圆的定义即可证得。
证明:(1)在![]() 中,由正弦定理可知
中,由正弦定理可知![]() ,则
,则![]() ∴
∴![]()
∴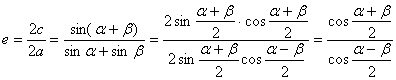
(2)在![]() 中由余弦定理可知
中由余弦定理可知
![]()
![]()
∴![]()
∴![]() 。
。
 例15、过点
例15、过点![]() 作直线
作直线![]() 与椭圆3x2+4y2=12相交于A、B两点,O为坐标原点,求△OAB面积的最大值及此时直线倾斜角的正切值。
与椭圆3x2+4y2=12相交于A、B两点,O为坐标原点,求△OAB面积的最大值及此时直线倾斜角的正切值。
分析:若直接用点斜式设![]() 的方程为
的方程为![]() ,则要求
,则要求![]() 的斜率一定要存在,但在这里
的斜率一定要存在,但在这里![]() 的斜率有可能不存在,因此要讨论斜率不存在的情形,为了避免讨论,我们可以设直线
的斜率有可能不存在,因此要讨论斜率不存在的情形,为了避免讨论,我们可以设直线![]() 的方程为
的方程为![]() ,这样就包含了斜率不存在时的情形了,从而简化了运算。
,这样就包含了斜率不存在时的情形了,从而简化了运算。
解:设A(x1,y1),B(x2,y2),![]() :
:![]()
把![]() 代入椭圆方程得:
代入椭圆方程得:![]() ,即
,即
![]() ,
,![]() ,
,![]()
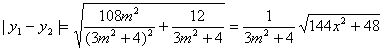
![]()
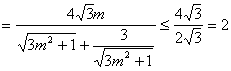
∴![]() ,此时
,此时![]()
![]()
令直线的倾角为![]() ,则
,则![]()
即△OAB面积的最大值为![]() ,此时直线倾斜角的正切值为
,此时直线倾斜角的正切值为![]() 。
。
【一周一练】
一、选择题
1、如果椭圆的焦距、短轴长、长轴长成等差数列,则离心率e为[ ]
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2、如果方程x2+ky2=2表示焦点在y轴上的椭圆,则实数k的取值范围是[ ]
A. (0,+∞) B. (0,2) C. (1,+∞) D. (0,1)
2、曲线![]() 与曲线
与曲线![]() 之间具有的等量关系:[ ]
之间具有的等量关系:[ ]
A. 有相等的长、短轴 B. 有相等的焦距
C. 有相等的离心率 D. 有相同的准线
4、P是椭圆![]() 上的一点,F1和F2是焦点,若∠F1PF2=30°,则△F1PF2的面积等于[ ]
上的一点,F1和F2是焦点,若∠F1PF2=30°,则△F1PF2的面积等于[ ]
A. ![]() B.
B.
![]() C.
C. ![]() D. 16
D. 16
5、设一动点P到直线x=5的距离与它到点A(1,0)的距离之比为![]() ,则动点P的轨迹方程是[ ]
,则动点P的轨迹方程是[ ]
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
6、设θ∈(![]() ),则关于x,y的方程x2cscθ-y2secθ=1所表示的曲线是[ ]
),则关于x,y的方程x2cscθ-y2secθ=1所表示的曲线是[ ]
A. 实轴在y轴上的双曲线 B. 实轴在x轴上的双曲线
C. 长轴在y轴上的椭圆 D. 长轴在x轴上的椭圆
7、椭圆25x2-150x+9y2+18y+9=0的两个焦点坐标是[ ]
A.(-3,5)(-3,3) B.(3,3)(3,-5)
C.(1,1)(-7,1) D.(7,-1)(-1,-1)
8、曲线y=![]() 与直线y=k(x-1)+3有交点时,实数k的取值范围是( )
与直线y=k(x-1)+3有交点时,实数k的取值范围是( )
A.(-∞,-7]∪(3-![]() ,+∞)
B.[-7,3-
,+∞)
B.[-7,3-![]() ]
]
C. (-∞,-7]∪[1,+∞) D. [-7,1]
二、填空题
9、过椭圆x2+2y2=2的焦点引一条倾斜角为45°的直线与椭圆交于A、B两点,椭圆的中心为O,则△AOB的面积为 ________________。
10、椭圆C与椭圆![]() ,关于直线x+y=0对称,则椭圆C的方程是___________________。
,关于直线x+y=0对称,则椭圆C的方程是___________________。
11、到两定点F1(3,0),F2(9,0)的距离和等于10的点的轨迹方程是 。
12、已知椭圆![]() 的离心率
的离心率![]() ,则a的值等于 _________。
,则a的值等于 _________。
三、解答题
13、△ABC中三边长度AB、BC、CA成等差数列,若B、C两点的坐标分别为B(3,0)C(-3,0),求顶点A的轨迹。
14、已知椭圆的焦点F1(-1,0)和F2(1,0),直线x=4是椭圆的一条准线,(1)求椭圆的方程;(2)设点P在这个椭圆上,且PF1-PF2=1,求cos∠F1PF2的值。
15、已知椭圆![]() ,直线
,直线![]() :
:![]() ,P是
,P是![]() 上一点,射线OP交椭圆于点R,又点Q在OP上且满足OQ·OP=OR2,当P在
上一点,射线OP交椭圆于点R,又点Q在OP上且满足OQ·OP=OR2,当P在![]() 上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
16、已知中心在原点,焦点在y轴上,长轴长等于6,离心率![]() ,试问是否存在直线
,试问是否存在直线![]() ,使
,使![]() 与椭圆交于不同两点A、B,且线段AB恰被直线
与椭圆交于不同两点A、B,且线段AB恰被直线![]() 平分?若存在,求出直线
平分?若存在,求出直线![]() 倾角的取值范围;若不存在,请说明理由。
倾角的取值范围;若不存在,请说明理由。
17、设椭圆的中心是原点,长轴在x轴上,离心率e=![]() ,已知点P(0,
,已知点P(0,![]() )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是![]() ,求这个椭圆方程,并求椭圆上到点P距离等于
,求这个椭圆方程,并求椭圆上到点P距离等于![]() 的点的坐标。
的点的坐标。
18、设椭圆C1:![]() (a>b>0),曲线C2:y=
(a>b>0),曲线C2:y=![]() ,且C1与C2在第一象限内只有一个公共点P,(1)试用a表示P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积,函数s (a)的值域;(3)证min{y1,y2……yn}为y1、y2……yn中最小的一个,设g (a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f (a)=min{g(a),s (a)}的表达式。
,且C1与C2在第一象限内只有一个公共点P,(1)试用a表示P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积,函数s (a)的值域;(3)证min{y1,y2……yn}为y1、y2……yn中最小的一个,设g (a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f (a)=min{g(a),s (a)}的表达式。
【一周一练答案】
一、选择题
1. A 2. D 3. B 4. B 5. C 6. C 7. B 8. A
二、填空题
9. ![]() 10.
10.![]()
11. ![]() 12. 4或
12. 4或![]()
三、解答题
13. ![]() 除点(6,0)(-6,0) 14. 1)
除点(6,0)(-6,0) 14. 1)![]() 2)cos∠F1PF2=
2)cos∠F1PF2=![]()
15. 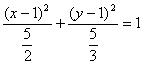 ,其中x、y不同时为零,轨迹是以(1,1)为中心,长短半轴分别为
,其中x、y不同时为零,轨迹是以(1,1)为中心,长短半轴分别为![]() 和
和![]() ,且长轴与x轴平行的椭圆,去掉坐标原点
,且长轴与x轴平行的椭圆,去掉坐标原点
16. x∈(60°,90°)∪(90°,120°)
17.椭圆方程为![]() ; 椭圆上点(-
; 椭圆上点(-![]() ,-
,-![]() )和(
)和(![]() ,-
,-![]() )到P点的距离都等于
)到P点的距离都等于![]() 。
。
18、1)P(![]() )
)
2)s (a)的值域为(0,![]() )
)
![]() 3)
a2-
3)
a2-![]()
![]() <a≤
<a≤![]()
f (a)=min{g (a), s(a)}=
![]() a>
a>![]()