无理不等式与绝对值不等式

姓名

班　级

学 号

时　间

课题

无理不等式与绝对值不等式

设　计

一、方法点拨：

（1）　　　　 掌握无理不等式的解法．在解的过程中注意两点：１．保证根式有意义，２．在利用平方去根号时，不等式两边要为非负数；

（2）　　　　 掌握绝对值不等式的解法．最简绝对值不等式分为两类：１．等价于或．２．等价于

要灵活准确地进行等价变形，并通过数形结合的方法理解不等式的几何意义．在解题过程中通过找出制约条件的相互关系，尽量减少列出的不等式的个数．

二、知能达标：

i.　 　 １不等式的解集为　　　　　　　　　　　　　

２．不等式的最小整数解是　　　　　　　　

３．不等式的解集为　　　　　　　　　　　

４．解不等式（１）；（２）；（３）

  ５．解关于ｘ的不等式：

６．设全集为R，集合A=，若求实数的取值范围．

7．某水库设计的最大容量为２６．２万立方米，库区的森林覆盖率为　　６０﹪，除森林外其余为裸露地．林地和裸露地分别有０．１和０．８５的雨水变成地表水流入水库．预测连续降雨，且单位面积降雨量相同，库区在ｘ天内降雨的总水量ｙ（单位为：万立方米）与天数ｘ之间的函数关系为，水库原有水量２０万立方米，在降雨的第二天就开始开闸泄洪，每天泄洪量为０．２万立方米．问连续降雨几天后，该水库就会发生险情（水库里水量超过设计的最大容量就有危险）．

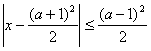8．若与（其中的解集依次为A与B，求使的的取值范围．