高考能力测试步步高数学基础训练17
基础训练17 线段的定比分点、平面向量的数量积及数量积
坐标表示、平移
●训练指要
掌握平面向量数量积的概念及性质,会用定比分点坐标公式解题.掌握平移含义,会求平移向量.
一、选择题
1.下面四个有关数量积的关系式:
①0·0=0,②(a·b)·c=a·(b·c),③a·b=b·a,④a·b≤a·b.
其中正确的是
A.①② B.②③ C.③④ D.①③
2.已知点P分有向线段![]() 所成的比是-3,则点P1分
所成的比是-3,则点P1分![]() 所成的比是
所成的比是
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-
D.-![]()
3.将函数y=2x的图象C按向量a=(-2,1)平移后得到图象C1,则C1的函数解析式是
A.y=2x-2+1 B.y=2x+2+1
C.y=2x+2-1 D.y=2x-2-1
二、填空题
4.若将向量a=(2,1)绕原点按逆时针方向旋转![]() ,得到向量b,则b的坐标是_________.
,得到向量b,则b的坐标是_________.
5.把函数y=log2(2x-3)+4的图象按向量a平移后得到函数y=log2(2x)的图象,则a=_________.
三、解答题
6.过两点A(-3,-1)和B(4,6)的直线与直线3x+2y-5=0交于点P,求点P分![]() 所成的比.
所成的比.
7.已知a=5,b=4,且a与b的夹角为60°,问当且仅当实数k为何值时,向量ka-b与a+2b垂直?
8.将函数f1(x)=x2-2x+2的图象F1按a=(h,k)平移后得到图象F2,F2对应的函数y=f2(x)的最小值是y=f1(x)最小值的2倍;若将F1按b=(k,h)平移后得到图象F3,F3对应的函数y=f3(x)的最小值与函数y=x+1+x-4的最小值相同,求h与k的值.
高考能力测试步步高数学基础训练17答案
一、1.D 2.B
提示:![]()
∴P1分![]() 所成的比为-
所成的比为-![]() .
.
3.B
二、4.(![]() )
)
提示:设![]() =a=(2,1),
=a=(2,1),![]() =b=(x,y),∠xOA=α,则∠xOB=α+
=b=(x,y),∠xOA=α,则∠xOB=α+![]() .
.
cosα=![]()
cosxOB=cosαcos![]() -sinαsin
-sinαsin![]() =
=![]() .
.
sinxOB=![]() .
.
又b=a=![]() ,
,
∴x=bcosxOB=![]() ,y=bsinxOB=
,y=bsinxOB=![]() .
.
∴b=(![]() ,
,![]() ).
).
5.(-![]() ,-4)
,-4)
提示:![]()
∴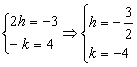
∴a=(-![]() ,-4).
,-4).
三、6.![]()
提示:设P分![]() 所成的比为λ,则
所成的比为λ,则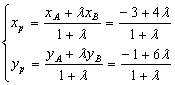
又3xp+2yp-5=0![]() λ=
λ=![]() .
.
7.![]()
8.k=1,h=4
提示:f1(x)=(x-1)2+1≥1,y=x+1+x-4≥5.
f2(x)=(x-h-1)2+1+k≥1+k,
f3(x)=(x-k-1)2+1+h≥1+h
∴![]()