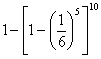| 姓名 | 班 级 | 学 号 | 时 间 | ||||
| 课题 | 相互独立事件乘积的概率与贝努里概型 | 设 计 | |||||
| 一、方法点拨: 1、 理解相互独立事件的概念,掌握独立事件乘积的概率乘法公式; 2、 掌握贝努里概型Pn(k)= 二、知能达标: 1、甲口袋内有大小相等的8个红球和4个白球,乙口袋内有大小相等的9个红球和3个白球,从两个口袋内各摸出一个球,那么 A、两个求都是白球的概率; B、两个求恰好有一个白球的概率; C、两个求都不是白球的概率; D、两个求不都是白球的概率; 2、10颗骺子同时掷出,共掷5次,则至少有一次全部出现一个点的概率是 ( ) A、 3、某人射击1次,击中目标的概率是0.8,他射击4次,至少击中3次的概率是 。 4、三人独立地破译一个密码,他们能译出的概率分别为 5、10根签中有3根彩签,设首先由甲、然后由乙各抽一签,求下列事件的概率 (1)甲、乙都中彩;(2)乙中彩。
| |||||||
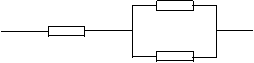
| 6、如图:三个元件a、b、c安置在线路中,各个元件发生故障是相互独立的,且概率分别为0.3、0.2、0.1,求线路由于元件发生故障而中断的概率。
7
8、已知某产品的优质品率为5﹪,攻关小组要想找一件优质品进行分析研究,问需要检验多少件产品,才能以90﹪的概率保证至少找到一件优质品? |
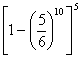 B、
B、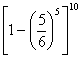 C、
C、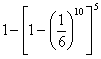 D、
D、