选择题的应对策略
复习目标:通过复习进一步掌握选择题的几种常见解法,要求在解选择题时做到一快,二准
一、答题要求
从命题的角度来看,一份数学试卷中的选择题都是用直接法求解,决不是一份好试卷,由于选择题不仅要担负检测“三基”的牢固程度,还担负着检测学生的思维敏捷灵活、快速的程度,故常要用到估算法、特例法、直觉思维法等等;从考试角度来看,一位同学解答一份试卷中的选择题都用直接法求解,往往导致“小题大作”,也决不会得到理想的分数,由于在解选择题过程中用时过多,就挤掉了后面考虑难题的时间,就是一种潜在丢分或隐含失分. 因此研究选择题的得分技巧必须做到:简捷快速.如何才能做到“简捷快速”,首先要了解选择题的三个特点:结构特征、担任角色及解法要求,然后才能有的放矢、抓住要害、获得简解.
选择题的结构特征与常规的解答题一样,有前提因素和结论因素,但更有自己的独特地方,可细分为四部分.
前提的组成是解题的信息源,它包含了三个部分:
⑴统一前提——所有的选择题的共同说明词,即“在每小题给出的四个选项中,只有一项符合题目要求的”. 也就是在四个选项中“有且只有一个正确”的单项选择题.
⑵具体前提——即题干,类似于解答题中的已知条件.
⑶选择前提——四个可供选择的答案,亦称选项,其中三个选项是错误的. 这是一个独特的条件,既有结论因素,又不象证明题那样明确指出,但确实有一个正确选项.
结论是第四部分,既简单又独特.
⑷选择结论——填上代号,就是根据“统一前提”、“具体前提”、“选择前提”找出结论的代号.
选择题的角色要求,对于知识要求包括了解、理解、掌握等三个层次,总体来说属于基本题,平均得分率0.7左右,具有单、多、广、活等特点,即内容比较单一、数量比较多、覆盖面比较广、题型(取材)比较活泼. 其作用是考查 基础知识的的是否理解,基本技能的是否熟练,基本运算是否准确,基本方法是否会用,考虑问题是否严谨,解题速度是否快捷.
据近年高考选择题命题特点是“多考一点想,少考一点算”,以及选择题的结构特征和知识特征,则其解法要求是要做到“小题小(巧)做”,避免“小题大(难)做”.否则就是潜在丢分或隐含失分.下面举例说明.
例1(2001年全国高考题) 过点A(1,-1)、B(-1,1)且圆心在直线x+y-2=0上的圆方程是( )
(A) (x-3)2+( y+1)2=4(B) (x+3)2+( y-1)2=4
(C) (x-1)2+( y-1)2=4 (D) (x+1)2+( y+1)2=4
解法1:(小题大做)
设圆的方程为![]() ,根据题意,得
,根据题意,得
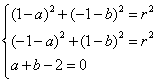 ,解得
,解得![]() ,故选(C).
,故选(C).
解法2:(小题大做)
设圆的方程为![]() =0,根据题意,得
=0,根据题意,得
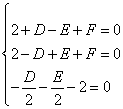 ,解得D=E=F=-2,故选(C).
,解得D=E=F=-2,故选(C).
评注解法1、2是利用圆的标准方程和一般方程求解与做一道解答题没有任何区别,选择题的特点体现不出来,是“小题大做”.
解法3:(小题小做)
因圆心在直线x+y-2=0上,设圆心为(a,2-a),又A、B在圆上,由圆的定义,有
![]() =
=![]()
解得a=1,圆心为(1,1),排除(A)、(B)、(D),而选(C).
解法4:(小题小做)
由选项(B)、(D)的圆心坐标不在直线x+y-2=0上,故排除(B)、(D);又选项(A)的圆不过点![]() ,又排除(A),故选(C).
,又排除(A),故选(C).
评注 解法3、4对知识的理解程度及选择题的特点已有所理解,由于四个选项的半径相等,只是圆心不同,故只需考虑圆心坐标即可,有解法3;解法4是利用逆推验证法.
解法5: (小题巧做)
由选项知,只要估算出圆心所在的象限即可.显然圆心应在线段AB的垂直平分线(即一、三象限的角平分线)上,又在直线x+y-2=0上,画草图知,交点(即圆心)在第一象限内,故选(C).
例2在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=()
(A) 12(B) 10(C) 8 (D) 2+log35
解法1(小题难做)从已知条件中求出a1,q(或说an的表达式),从而逐项求出log3a1,log3a2,…,log3a10,再相加.由于条件中a5a6=9不能唯一确定一个数列,故此法无法办到.
解法2(小题大做)由已知9=a5a6=(a1q4)(a1 q5)=![]() ,则
,则
a1a2…a10=![]() =
=![]() =310.
=310.
故原式=log3(a1a2…a10)=log3310=10,因而选(B).
评注此解法与做一道数列解答题没有任何区别,是典型的“小题大做”.
解法3(小题小做)由已知9=a5a6=a4a7=a3a8=a2a9=a1a10,
故原式=log3(a5a6)5=log3310=10,因而选(B).
评注此解法对等差数列知识的理解有所深化,但仍没有充分利用选择题的结构特点和回答方式上的特点.
解法4(小题巧做)由结论暗示,不管数列{an}的通项公式是什么(有无穷多个),答案都是唯一的,故只需取一个满足条件的特殊数列an=3,知选(B).
从上面两例可以看出,解题是有技巧可言,不同方法技巧的选择,会影响解题的速度. 小题巧(小)解能节省大量时间,能在一二分钟内解决问题, 甚至是十几秒. 如何才能做到此点,下面例析快速选择技巧.
二 、快速选择技巧
基于选择题的特点,解选择题有两条重要思路:一是肯定一支,二是否定三支 .下面例析如何运用此两条思路,进行选择题的快速选择
1、 直接选择法
直接从题设出发,通过推理和准确的运算得出正确的答案再与选择的答案支对照比较,从而判定正确选择支。它一般步骤是:计算推理、分析比较、对照选择。它又可分为两个层次:
①直接判定法
有些选择题结构简单,常可从题目已知入手,利用定义、定理、性质、公式直接指出正确答案。多用于解答有关基本概念或简单性质辨析的选择题。
②求解对照法
对于涉及计算或证明的选择题,有时可采用求解对照法。其基本思想是把选择题当作常规题来解,然后与题目选择支相对照,选出正确答案。
例3设有三个函数,第一个函数是![]() ,它的反函数是第二个函数,而第三个函数与第二个函数图象关于
,它的反函数是第二个函数,而第三个函数与第二个函数图象关于![]() 对称,那么第三个函数是 ( C )
对称,那么第三个函数是 ( C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:![]() 故选(C)
故选(C)
例4、设![]() 都是正数,且
都是正数,且![]() ,那么
( B )
,那么
( B )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:令![]() =k,取对数
=k,取对数![]() ,由
,由![]()
可得![]() , 故选(B)
, 故选(B)
2、 估算选择法
估算是用于解答选择题的一种简捷方法,它是指通过大体估值、合理猜想或特殊验证等手段,准确、迅速地选出答案的方法.充分体现了小题小(巧)做的解题策略.在近年高考的“多想少算”命题思想中,“估算法”更是解决此类问题的有效途径,常有以点估式(图)、以部分估整体、以范围估数值等.
例5(1999年全国高考题)如图1,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,![]() ,EF与面AC的距离为2,则多面体的体积为()
,EF与面AC的距离为2,则多面体的体积为()
A. ![]() B. 5C. 6D.
B. 5C. 6D. ![]()
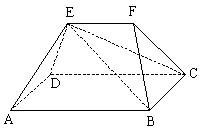
图1
分析:本题的背景是非典型的多面体,需对图形进行分解、组合.连EB、EC,得一个四棱锥E—ABCD和一个三棱锥E—BCF,结合选项可知:用易求的部分体积“四棱锥E—ABCD”估整体法,极其简捷.
解: 本题可用部分估整体法,连EB、EC,则易得
![]()
故排除A、B、C,应选D
评注:以部分估整体是指欲求结论由若干部分(或元素)构成时,研究易求的部分(或元素)而进行排除错肢,从而快速选答.
例6若四面体各棱长是1或2,且该四面体不是正四面体,则其体积的值不可能是 ( )
A、![]()
![]() B、
B、![]() C、
C、![]() D、
D、![]()
例7正方体的全面积是![]() ,它的顶点都在球面上,这个球的表面积是()
,它的顶点都在球面上,这个球的表面积是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
分析:此题如“不看选项,只看题干”,则变成普通的求解题,可以预见运算量不少,恐怕很难心算而得到结果,然而将“题目与四选项相结合”,用范围来估算,几乎人人都能一望而答——这就是估算法的魅力.
解:外接球的表面积,比起内接正方体的全面积来,自然要大一些,但绝不是它的约6倍(C)或约9倍(D),也不可能与其近似相等(A),故选B.
3、 特例选择法
高考数学选择题是四选一型的单项选择题,对于条件或结论是一般性问题,“特例选择法”是行之有效的方法.此法的主要特征是取特例(如特殊值、特殊函数、特殊角、特殊点、特殊数列等等),进行合理科学的判断——否定或肯定,从而达到快速解题目的.
例8(2002年全国高考题) 不等式(1+x)(1-│x│)>0的解集是( )
(A) {x│0≤x<1} (B) {x│x<0且x≠-1}
(C) {x│-1<x<1} (D) {x│x<1且x≠-1}
分析 本题若用直接法,需分类讨论,计算量大且易出错.而用特殊值法,则能省时又省力.
解:取x=0、-2,显然是原不等式的解,故排除(A)(B)(C),而选(D).
例9若a,b,c成等比数列,m为a、b的等差中项,n为b、c的等差中项,则![]() 的值为
( )
的值为
( )
A、4 B、3 C、2 D、1
例10(1997年高考试题)不等式组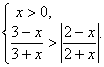 的解集是
( C )
的解集是
( C )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
题目设计的四选择支数据:2、![]() 、2.5、3四个数值非常接近。让学生不易取值排除。但聪明的发现将x=
、2.5、3四个数值非常接近。让学生不易取值排除。但聪明的发现将x=![]() 代入能使不等式两边相等为
代入能使不等式两边相等为![]() ,考虑不等式解与方程有关,猜答案为(C)
,考虑不等式解与方程有关,猜答案为(C)
4、 特征选择法
特征分析选择法是指通过认真地审题,深入挖掘问题的不同特征,将隐含条件、内部结构等显露出来,从而把握住问题脉搏、优化思维,开拓快速解题的捷径.我们可从以下几个方面去分析:条件特征的分析、结论特征的分析、位置特征的分析、结构特征的分析、语言特征的分析等.
例11(1999年全国高考题)若![]() ,则
,则![]() 的值为()
的值为()
A. 1 B. ![]() C. 0 D. 2
C. 0 D. 2
解:考察待求式结构
![]()
恰是条件![]() 结构中,取特殊值
结构中,取特殊值![]() 与
与![]() 时的积.
时的积.
即![]() ,故选A
,故选A
说明:纵观问题的条件与结论,某些命题的已知数式结构中常常隐含着某种特殊的关系,通过细致而敏锐的观察,进而联想转化,可实现解题的选择.
例12设![]()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]() ( )
( )
5、直观选择法
直观选择法就是通过数形结合的方法,借助图形的直观性,迅速作出判断的一种解题方法.常用的图形有:韦恩图、数轴、三角函数线、函数的图像、方程的曲线、几何图形、表格等.
例13已知α为锐角,且cosα=3/5,cos(α+β)=-5/18,那么β是第( )象限的角
A、一 B、一或二 C、一或三 D、二或三
6、结论选择法
由于高考命题原则是“源于教材,而略高于教材”,加上选择题是不必说明理由等特点. 在数学学习过程中可总结出略高于教材的真命题,但又不是课本中的定理、公式,故我们称它们为规律性结论. 利用它可大大简化解题过程,掌握一定量的规律性结论是很有必要的.对于规律性同学们可根据自己的实际情况加以总结.
例14(1998年全国高中数学联赛题)各项都是实数的等比数列{an},前n项的和记为Sn,若S10=10,S30=70,则S40等于()
(A) 150 (B) -200 (C) 150或-200 (D) 400或-50
分析 等比数列{an}的公比为q,前n项和为Sn,则得等比数列又一一求和公式Sm+n=Sm+qmSn.
解法1由“另一求和公式”,得S40=S30+q30S10.
又S30>0,q30>0,S10>0.
∴ S40>0,排除(B)、(C)、(D),而选(A).
解法2由公式,得S30=S20+q20S10=S10+q10S10+q20S10.
从而有q20+q10-6=0,解得q10=2.
∴ S40=S30+q30S10=70+8×10=150,选(A).
7、逆代验证
例15、(1994年高考文科卷)如果函数![]() 的图象关于直线
的图象关于直线![]() 对称,那么
( D )
对称,那么
( D )
(A)![]() (B)-
(B)-![]() (C)1 (D)-1
(C)1 (D)-1
分析:本题难度系数0.3。许多人在化到![]() 不知如何下手。应注意其对称轴过图象波峰波谷,即最值处。将
不知如何下手。应注意其对称轴过图象波峰波谷,即最值处。将![]() 代入有
代入有
![]() 。采用将各值代入验证排除更易推出选(D)
。采用将各值代入验证排除更易推出选(D)
例16若向量m=(2,0),n=(3,0),a-m=![]() ,a-n=4,则向量a为 ( )
A、(-3,±4) B、(4,
±3)
C、(3, ±4) D、(-4,
±3)
,a-n=4,则向量a为 ( )
A、(-3,±4) B、(4,
±3)
C、(3, ±4) D、(-4,
±3)
8、逻辑分析
根据提供的选择支结合题意,通过分析确定正确答案。
例17已知集合![]() ,那么
,那么![]() 为区间
( A )
为区间
( A )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:(A)(C)排斥,(B)(D)排斥,在(B)中取![]() 无意义,排除(B),在(D)中取
无意义,排除(B),在(D)中取![]() 排除(D)同时也排除(C) 故选(A)
排除(D)同时也排除(C) 故选(A)
例18下列四个命题中的假命题是 ( )
A存在无穷多个![]() ,使得
,使得![]()
B不存在无穷多个![]() ,使得
,使得![]()
C对任意![]() ,使得cos(
,使得cos(![]() )=
)=![]()
D、不存在这样的![]()
三、解题注意点
解题时,若根据题设推出的结果与选择支都不相同,说明解题有误,须认真检查每个解题环节,找出错误的原因。有时由于概念不清或计算不慎,所得结果与某一干扰支相同,这样陷入“陷阱”。为识破命题者的“陷阱”,提高解选择题的正确率,再强调以下几点:
1、审题要仔细
审题时要逐字逐句推敲,分析隐含条件,掌握关键词句。
例19、已知x1,x2是方程![]() 的两实根,则
的两实根,则
![]() 最大值是
( B )
最大值是
( B )
(A)19 (B)18 (C)![]() (D)不存在
(D)不存在
分析:由![]() 若忽略两实根
若忽略两实根![]() 的约束,易错选(A)
的约束,易错选(A)
事实上解出![]() 时,最大值为18
时,最大值为18
例20、已知![]() 求
求![]() 的值
( C )
的值
( C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:若充分注意到题设中的隐含条件![]() ,可判断
,可判断
![]() ,从而判定
,从而判定![]() ,可直接选出(C),避免了产生增根错选(A)
,可直接选出(C),避免了产生增根错选(A)
2、基础要牢靠
选择题小、巧、活的特点。是检查基础知识,考察判断力的好题型。为解题正确而迅速,必须牢固掌握教材中的基础知识。概念不可混淆不清,性质不可似是而非,方法不可模棱两可。
例21、若函数f(x+1)的定义域是[1,2],f(x-2)的定义域是 ( B )
(A)[3,4] (B)[4,5] (C)[2,3] (D)[-2,-3]
分析:对函数定义域及复合函数的意义要充分理解,才不至模棱两可。
3、分析要全面
分析不全面,有时会使符合题意的解出现重复或遗漏,有时又会让不合题意的解鱼目混珠。
例22、与空间四点等距的平面至少有 ( D )
(A)1个 (B)3个 (C)4个 (D)7个
例48、(97年)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有 ( D )
(A)150种 (B)147种 (C)144种 (D)141种
解:本题为近年高考中得分最低的选择题。任取4点有![]() 种,其中4点共面的情况有三类。一类:4点位于四面体的同一面内,有
种,其中4点共面的情况有三类。一类:4点位于四面体的同一面内,有![]() 种;二类:中位线构成的平行四边形,有3种;三类:取一棱上3点及对棱的中点,有6种。(最易忽略)故取法有:
种;二类:中位线构成的平行四边形,有3种;三类:取一棱上3点及对棱的中点,有6种。(最易忽略)故取法有:![]() -
-![]() -3-6=141,选(D)
-3-6=141,选(D)
例23、从1~9这九个数字中任取两个不同的数分别作对数的真数和底数,可得不同的对数值有 ( B )
(A)32 (B)53 (C)57 (D)72
例24、若函数![]() 的图象在x轴上方,则实数
的图象在x轴上方,则实数![]() 的取值范围 制 ( B )
的取值范围 制 ( B )
(A)(1,19) (B)[1,19) (C)[1,19] (D)以上不对
略析:一定要考虑![]() 函数退缩为常函数
函数退缩为常函数![]() 也满足条件,故选(B)
也满足条件,故选(B)
例25、长方体ABCD-A1B1C1D1中,AB=3,BC=2,A1A=1,则从A点出发沿表面到C1的最短距离是 ( C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
略析:侧面展开要考虑到两种路径再比较大小。选(C)
4、方法要灵活
不要把选择题简单地等同于填空题、计算题、证明题。要充分注意用题目提供的信息,灵活运用各种解法,避繁就简,才能事半功倍。
例26、P是边长为2的正方形内切圆圆周上一点,P对正方形两对角线视角分别是![]() ,则
,则![]() 的值
( C )
的值
( C )
(A)2 (B)4 (C)8
(D)![]()
解:抓住特点用特殊值法,可迅速求解。不妨取P点为正方形对角线与它的内切圆的交点,不难求得:![]() ,代入得
,代入得![]() =8
=8
例27、曲线![]() 与直线
与直线![]() 有两交点时,实数
有两交点时,实数![]() 的取值范围
( A )
的取值范围
( A )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:首先数形结合作出两函数图象,前者为圆心为(0,1)半径为2的上半圆,后者为过定点(2,4)的直线系。如图。有两交点需![]() 故排除(B)、(D)。那么切线
故排除(B)、(D)。那么切线![]() 到底是
到底是![]() ,由选择支中反复出现的
,由选择支中反复出现的![]() 已暗示了答案可能是(A),可进一步代值,由圆心到直线的距离等于半径来验证
已暗示了答案可能是(A),可进一步代值,由圆心到直线的距离等于半径来验证![]() 故选(A)
故选(A)
|
|
例28、梯子10级,一步上一级或2级,规定8步走完有多少种走法 ( B )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:设2级需x步,1级y步,有![]() x=2,y=6即10=2
x=2,y=6即10=2![]() 2+6
2+6![]() 1,进一步研究2步2级的不同位置,故为
1,进一步研究2步2级的不同位置,故为![]() 。选(B)
。选(B)
四、选择题练习:
1、x2+y2-4x+2y+f=0与y轴交于A、B两点。圆心为C,若![]() ,则f的值为
( )
,则f的值为
( )
![]()
![]()
![]() D、—3
D、—3
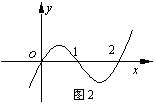
2、(2000年北京春季高考题)已知函数![]() 的图像如图2,则()
的图像如图2,则()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
分析:由图像过特殊点的特征,可得以下式子:
(1)![]() ,即
,即![]() ;
;
(2)![]() ,即
,即![]()
(3)![]() ,即
,即![]()
(4)![]()
(5)当![]() 时,
时,![]() ,有
,有![]() ,即
,即![]() ;
;
(6)当![]() 时,
时,![]() ,有
,有![]() ,得
,得![]() .
.
巧妙合理地运用以上式子,即可得到多种简洁解法.
解法1:由(2)、(3)解得![]() ,又由(6)知
,又由(6)知![]() ,故选A.
,故选A.
解法2:由(2)+(5)得,![]() ,即
,即![]() ,故选A.
,故选A.
解法3:由(4),比较同次项系数,得![]() ,又
,又![]() 知
知![]() ,而选A.
,而选A.
解法4:由(4),取特殊函数![]() ,得
,得![]() ,而选A.
,而选A.
说明:很多抽象的数量关系,一旦转化为具体的图形问题,则思路与方法便从图形中直观地显示出来,反之抓住给出图形过特殊点、特殊位置,往往能优化解题.故抓住图形特征,有助于快速解题.
3、设a、b是满足ab<0的实数,那么 ( )
A、a+b>a-b B、a+b<a-b C、a-b<a-b D、a-b>a+b
4、正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别为SC、AB的中点,则异面直线EF与SA所成的角为 ( )
A、 900 B、600 C、450 D、300
5、对 任何α∈(0,π/2),都有 ( )
A、sinsinα<cosα<coscosα B、sinsinα>cosα>coscosα
C、sincosα<cossinα<cosα D、sincosα<cosα<cossinα
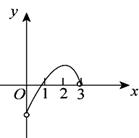
6、(2002年北京高考题) 已知f(x)是定义在(-3,3)上奇函数,当0<x<3时,f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是()
(A)(-3,-![]() )∪(0,1)∪(
)∪(0,1)∪(![]() ,3)
,3)
(B) (-![]() ,-1)∪(0,1)∪(
,-1)∪(0,1)∪(![]() ,3)
,3)
(C)(-3,-1)∪(0,1)∪(1,3)
(D) (-3,-![]() )∪(0,1)∪(1,3)
)∪(0,1)∪(1,3)
分析:直接解此不等式,显然较难且是小题大做.本题可取特殊值法排除错支,而得到正确答案.
解:取x=-2,则有f(x)cosx=f(-2)cos(-2)=-f(2)cos2>0,即x=-2,不满足f(x)cosx<0,故排除(A)(C)(D),而选(B).
7、在各项均为正数的等比数列{ an}中,若a5a6=9,则log3a1+log3a2+……+log3a10等于 ( )
A、12 B、10 C、9 D、2+log35
8、 (2003年北京春季高考题)若A,B,C是ΔABC的三个内角.且A<B<C(C≠![]() ),则下列结论正确的是()
),则下列结论正确的是()
(A) sinA<sinC (B) cosA<cosC
(C) tanA<tanC (D) cotA<cotC
分析:本题可用取特殊三角形排除错支,而得到正确答案.
解:取A=30°,B=40°,C=110°,显然排除 (B)、(C) 、(D),而选(A).
9、1、2、3、4、5五个数字,可以组成比20000大,并且百位数字不是3的没有重复数字的五位数( )个。
A、96 B、78 C、72 D、64
10、在某两个正数x、y之间,若插入一个正数 a,使x、a、y成等比数列,若插入两个正数b、c,使x、b、c、y成等差数列,则关于t的一元二次方程bt2-2at+c=0 ( )
A、 两个相等实根 B、有两相异实根
C、无实根 D、有两个相等实根或无实根
11、在等差数列{an}中,已知an=m,am=n(n![]() m,m、n
m,m、n![]() N),则am+n= ( )
N),则am+n= ( )
A、0 B、m C、n D、n+m
12、小船在相距S的两地A、B之间航行,若已知小船在静水中航速为V,河水流速为U,则小船在A、B之间往返一次,其平均速度为 ( )
A、大于V B、小于V C、等于V D、无法判断
13、设a、b是空间的两条直线,它们在平面![]() 上的射影是两条相交直线,它们在平面
上的射影是两条相交直线,它们在平面![]() 上的射影是两条平行直线,它们在平面
上的射影是两条平行直线,它们在平面![]() 上的射影是一条直线与直线外的一点,则这样的平面
上的射影是一条直线与直线外的一点,则这样的平面![]() 有
( )
有
( )
A、0 B、1 C、2 D、无数多个
14、已知![]() ( )
( )
A![]() B
B ![]() C
C ![]() D
D ![]()
15、从正方体的棱和各个面上的对角线中选出k条,使得其中任意两条线段所在的直线都是异面直线,则k的最大值为 ( )
A、2 B、3 C、4 D、6
16、已知f(x)=![]() 且f(-1)=1.62,则f(1)的值约为 ( )
且f(-1)=1.62,则f(1)的值约为 ( )
A 0.38 B 1.62 C 2.38 D 2.62
 y P C A B O X
y P C A B O X