选择题解法
一、直接求解法：
1、已知f(x)=x(sinx+1)+ax2,f(3)=5,则f(－3)=………………………………………………………( )
(A)－5 (B)－1 (C)1 (D)无法确定
2、若定义在实数集R上的函数y=f(x+1)的反函数是y=f－1(x－1),且f(0)=1,则f(2001)的值为…( )
(A)1 (B)2000 (C)2001 (D)2002
3、已知奇函数f(x)满足：f(x)=f(x+2)，且当x∈(0,1)时，f(x)=2x－1,则
的值为……（ ）
(A)－
（B）－
（C）－
（D）－
4、已知两点M(1,
),给出下列曲线方程：①4x+2y－1=0；②x2+y2=3；③
； ④
.在曲线上存在点P满足MP=NP的所有曲线方程是…………………………（ ）
（A）①③ （B）②④ （C）①②③ （D）②③④
5、设a>b>c,n∈N,且
恒成立，则n的最大值是…………………………（ ）
(A)2 (B)3 (C)4 (D)5
6、如果把y=f(x)在x=a及x=b之间的一段图象近似地看作直线的一段，设a≤c≤b，那么f(c)的近似值可表示为……………………………………………………………………………………………（ ）
(A)
(B)
(C)
(D) 
7、如果椭圆经过原点，焦点为（1，0）与（3，0），则离心率为………………………………（ ）
(A)
(B)
(C)
(D)
8、A={1，2，3}，B={4，5，6}，若从A到B的映射
满足1的象为4，则这样的映射有（ ）
(A)2个 (B)4个 (C)8个 (D)9个
9、等差数列{an}的公差为d，前n项和为Sn=－n2，则有………………………………………（ ）
(A)
=2n－1，d=－2 (B)=2n－1，d=2
(C)=－2n＋1，d=－2 (D) =－2n＋1，d=2
10、△ABC中，3sinA＋4cosB=6，4sinB＋3cosA=1，则角C的大小是…………………………（ ）
(A)
(B)
(C) 或 (D)
或
二、逆推验证法（利用选择支的结论进行逆推）：
11、若不等式0≤x2－ax+a≤1的解集是单元素集，则a的值为……………………………………（ ）
(A)0 (B)2 (C)4 (D)6
12、如果函数y=sin2x+a cos2x的图象关于直线x=－
对称，那么a=……………………………( )
(A)
(B)－
(C)1
(D)－1
13、已知复数z满足z+z·
,则复数z的值是……………………………………………( )
(A)
(B)
(C)
(D)
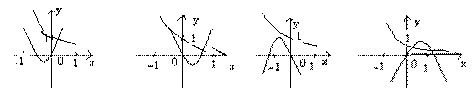14、在下列图象中，二次函数y=ax2+bx与指数函数
的图象只可能是………………（
）
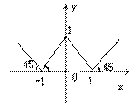
15、f(x)是定义在R上的奇函数,且f(3－x)=f(3+x),若 x∈(0,3)时f(x)=2x,则f(x) 在(－6,－3)上的解析式是f(x)=……………………………………………………………………………………………（ ）
（A）2x+6 （B）－2x+6 （C）2x （D）－2x
16、已知y=f(x)的图象如右，那么f(x)=……………………………………( )
(A)
(B)
(C)x2－2x+1 (D)x2－1
三、特例检验法：取满足条件的特例（特殊值、特殊点、特殊图形等）进行推证。
17、集合A和B都是正整数集合，映射
把集合A中的元素n映射到B中的元素2n＋n，则在此映射下，20的原象是………………………………………………………………………（ ）
（A）2 （B）3 （C）4 （D）5
18、不等式组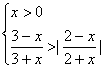
的解集为……………………………………………………………（ ）
（A）{x0<x<2} （B）{x0<x<2.5}
（C）{x0<x<
} （D）{x0<x<3}
19、在[0，2
]上，满足
的x的范围是……………………………………………………（ ）
（A）[0，] （B）[，] （C）[，] （D）[，]
20、函数y=f(x)在（0，2）上是增函数，函数y=f(x＋2)为偶函数，则有………………………（ ）
(A)
<
<
(B)<< (C)<< (D)<<
21、不等式
的解集为…………………………………………………（ ）
（A）R+ （B）空集
（C）{xx
} （D）R—
22、直线l与抛物线y2=2px相交于A、B两点，O为原点，如果OA垂直于OB，则l一定过（ ）
（A）（
，0） （B）（p，0） （C）（2p，0） （D）（3p，0）
23、已知f(x)=
+1(x≥1).函数g(x)的图象沿x轴负方向平移1个单位后，恰好与f(x)的图象关于直线y=x对称，则g(x)的解析式是………………………………………………………………（ ）
（A）x2+1(x≥0) (B)(x－2)2+1(x≥2) (C) x2+1(x≥1) (D) (x+2)2+1(x≥2)
24、在三角形ABC中，A=2B，则sinBsinC＋sin2B=…………………………………………………( )
(A)sin2A (B)sin2B (C)sin2C (D)sin2B
25、若(1－2x)8=a0＋a1x＋a2x2＋…＋a8x8,则a0＋a1＋a2＋…＋a8=……………………………( )
（A）1 （B）－1 （C）38－1 （D）28－1
26、数列1,1＋2,1＋2＋22,…,1＋2＋22＋…＋2n－1,…的前99项的和是…………………………（ ）
（A）2100－101 （B）299－101 （C）2100－99 （D）299－99
四、逻辑分析法：
27、集合M={（x，y）x＋y=2}，N={（x，y）x－y=4}，则M
N=…………………………（ ）
(A)x=3，y=－1 (B)（3，－1） (C){3，－1} (D){（3，－1）}
28、满足
的一个x的范围是……………………………………………………………（ ）
(A)（0，
） (B) [0，] (C) [，
] (D) [，]
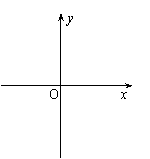
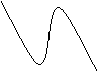
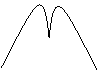
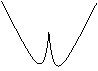
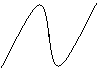
29、函数y=－xcosx的部分图象是……………………………………………………………………（ ）
 | |||||||
 |  |  | |||||
30、当x∈[－4,0]时
恒成立,则a的一个可能值是………………………( )
(A)5 (B)－5 (C)
(D)－
31、如果点（sinx－cosx，tanx）在第一象限，则在[0，2]内角x的取值范围是………………（ ）
(A)(，
)
(,
) (B)(,)(,) (C) (,)(,
) (D) (,)(,)
32、已知y=
为奇函数，当x>0时，=
，则x<0时，=………………（ ）
(A)－
(B) 
(C)－ (D)
33、集合A={
cos<sin,0
2},B={sin<tan,02}，则AB=…………（ ）
(A)(0, )(,2)
(B) (0,)( ,)
(C) (,)( 
,) (D) (,)( ,)
34、下列函数中，最小正周期为的偶函数为……………………………………………………（ ）
(A)y=sin2x
(B)y=
(C)y=sin2x＋cos2x (D)
五、数形结合法:明确条件及结论的几何意义,借助直观图形肯定或否定.
35、方程lg(x+4)=10x的根的情况是…………………………………………………………………( )
(A)仅有一根 (B)有一正一负根 (C)有两负根 (D)无实根
36、已知抛物线x2=y＋1上三点A、B、C，A（－1，0），AB⊥BC，当点B在抛物线上运动时，点C的横坐标的取值范围是…………………………………………………………………………（ ）
(A)(－
,－3][1,＋) (B) (－,－3) (C) [1,＋) (D)[－3,1]
37、当x∈（0，）时，不等式
恒成立，则实数a的取值范围是…………………（ ）
(A)[1,＋∞) (B) (1,＋∞)
(C) (
,＋∞) (D) [,＋∞)
38、E、F分别是正四面体S—ABC的棱SC、AB的中点,则异面直线EF与SA所成的角是…（ ）
(A)90o (B)60o (C)45o (D)30o
39、设m是方程
的解，n是方程
的解，则m＋n=………………………（ ）
(A)1 (B)2 (C)3 (D)6
40、函数f(x)=
在区间(－2,+ ∞)上为增函数,则a的取值范围是……………………………( )
(A)0<a<
(B)a<－1或a>
(C)a> (D)a>－2
41、已知函数f(x)=3－2x,g(x)=x2－2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x)=g(x);当f(x)<g(x)时,F(x)=f(x).那么F(x)………………………………………………………………………………（ ）
(A)有最大值3,最小值－1
(B)有最大值7－2
,无最小值
(C) 有最大值3,无最小值 (D) 无最大值,也无最小值
42、ω是正实数，函数f(x)=2sinωx在
上递增，那么……………………………………( )
(A)0<ω<
(B)0<ω≤2 (C)0<ω≤
(D) ω≥2