高三数学期末复习（三）
1．在平面直角坐标系内，将直线l按向量a=（－3，2）平移后，得到直线
与
间的距离为
，则直线l的倾斜角为 （ ）
A．
B．
C．
D．
2．如果直线
与圆
交于M、N两点，且M、N关于直线
对称，则不等式组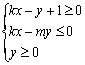
表示的平面区域的面积是 A．1 B．
C．
D．
3．设
为椭圆
的左、右焦点，过椭圆中心任作一直线与椭圆交于P、Q两点，当四边形
面积最大时，
的值等于 （ ）
A．0 B．1 C．2 D．4
4．设P是双曲线
右支上一点，F是该双曲线的右焦点，Q是PF的中点，O为坐标原点，且
，则点P到该双曲线右准线的距离为 （ ）
A．
B．
C．2 D．6
5．下列图中的多边形均为正多边形，M、N是所在边上的中点，双曲线均以图中的
为焦点，设图（1），（2），（3）中的双曲线离心率分别为
，则（ ）
 |
A．
B．
C．
D．
6．点
在圆
外，则直线
与圆的位置关系是 （ ）
A．相离 B．相切 C．相交 D．不确定
7．过抛物线
焦点的直线交抛物线于A、B两点，已知AB=10，O为坐标原点，则△OAB重心的横坐标为 .
8．双曲线两条渐近线的夹角为60°，该双曲线的离心率为 .
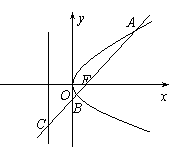9．若直线
过圆
的圆心，则
的最小值为 .
10．如图，过抛物线
的焦点F
的直线l交抛物线交于点A，B，交其准线于点
C，若
，且
，则此抛物线
的方程为 .
11．已知点A、B、C是椭圆
上的三点，且点A的坐标为
过椭圆m的中心，且
，
.
（1）求椭圆m的方程；（2）过点
的直线l（斜率存在不为零）与椭圆m交于两点E，F，设D为椭圆m与y轴负半轴的交点,且
，求实数t的取值范围.
12．已知i,
j分别是直角坐标系内x轴与y轴正方向上的单位向量，O为坐标原点，a为实数，经过定点
，以
为方向向量的直线l与曲线
相交于P、Q两点.
（1）实数a为何值时，
？
（2）是否存在a的值，使
？若存在，求出a；若不存在，说明理由.