数学奥林匹克高中训练题（21）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题26)
的关系为(B)．
(A)
(B)
(C)
(D)不能比较大小
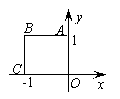2．(训练题26)已知函数
在
上的值域为
，则点
的轨迹为图中的(A)．
(A)线段
(B)线段
(C)线段
(D)线段
3．(训练题26)设三角形三个内角的对边分别为
，如果
，那么，下列等式中不成立的是(D)．
(A)
(B)
(C)
(D)
4．(训练题26)与三角式
恒等的是(A)．
(A)
(B)
(C)
(D)
5．(训练题26)给定四棱锥
，其中底面四边形
不是平行四边形，用平面截四棱锥得四边形
（
分别在侧棱
上），记集合
{四边形为平行四边形}，则有(B)．
(A)
为空集 (B)为无穷集合 (C)为单元集合 (D)的元素与底面形状有关，不能确定
6．(训练题26)红，黄，蓝变色灯的拉线开关是这样设计的：接上电源即出红色，拉第一次开关时灯色由红变黄，拉第二次时灯色由黄变蓝，拉第三次开关时灯色由蓝变红，如此循环往复．现对编号为
的
盏变色灯通上电源，先将编号为2的倍数的灯线拉一下，然后将编号为3的倍数的灯拉一下，最后将编号为5的倍数的灯拉一下后，拉完后黄色灯的盏数为(C)．
(A)
(B)
(C)
(D)
二、填空题（本题满分54分，每小题9分）
1．(训练题26)已知
，则
的值域为 1
．
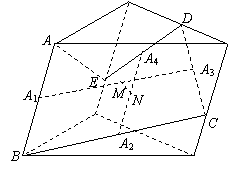
2．(训练题26)如图，三棱柱上有一个空间五边形
的中点为
的中点为
的中点为
的中点为
，连
是
的中点，
是
的中点，则
．
 |
3．(训练题26)双曲线
与
的交点为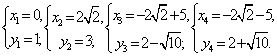
．
4．(训练题26)对
的每一个非空子集
，我们将中每一个元素
都乘以
然后求和．则所有的这此和的总和为
．
5．(训练题26)不等式
的解集为 
．
6．(训练题26)有
名乒乓球选手进行单循环赛（无和局），比赛结果显示：任意5人中既有1人胜于其余4人，又有1人负于其余4人.则恰胜两场的人数为
1 个．
三、(训练题26)(本题满分20分)对于曲线
上原点之外的每一点
，求证存在过的直线与椭圆
相交于两点
，使
均为等腰三角形．
四、(训练题26)(本题满分20分)已知直线
两两成异面直线，问是否存在直线
同时与相交？证明你的结论．
五、(训练题26)(本题满分20分) 某县位于沙漠地带，人与自然长期进行顽强的斗争，到1996年底全县的绿化率已达到30%（成为绿洲），从1997年开始，每年将出现这样的局面，原有沙漠面积的16%被栽上树，改造为绿洲，而同时，原有绿洲的面积的4%又被侵蚀，变为沙漠．(1)设全县面积为1，1996年底绿洲面积为
，经过
年绿洲面积为
，求证：
.(2)至少需经过多少年的努力才能使全县的绿化率超过60%(年取整数)？ 5
第二试
一、(训练题26)(本题满分50分)在锐角
中，
是
上的高，
是
边上一点，满足
，求证：
的充要条件是
．
二、(训练题26)(本题满分50分)已知复数
的模为1，求
的最大值．
三、(训练题26)(本题满分50分)将直线上的
点染成红色，
点染成黄色，
点染成蓝色，使同色点互不相邻，其染色方法的种数记为
，显然有
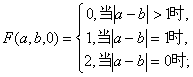
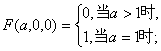
(1)证明：对不全为1的自然数有
(2)利用上述递推关系求解下题：
书架上有4本不同的数学书，5本不同的物理书，3本不同的化学书，全部竖起排成一行，如果要求同类书本身互不相邻邦，共有多少种排法？