数学奥林匹克高中训练题（23）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题28)对
，记
，
．则
与
的关系为(C)．
(A)
(B)
(C)
(D)不能确定，与
有关
2．(训练题28)已知函数
的定义域为
，值域为
．则的取值为(D)．
(A)区间
(B)区间
(C)区间
(D)集合
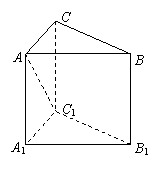
3．(训练题28)如图１，几何体
中，
，则
三线共点的充要条件是(C)．
(A)
(B)
(C)
(D)面
与面
不平行
4．(训练题28)
是公差为
的等差数列，则数列中任（不同）两项之和仍是这个数列中一项的充分必要条件是(A)．
(A)存在整数
，使得
(B)
(C)
为整数，
(D)
5．(训练题28)
是抛物线
上的四点，且满足
.则有(A)．
(A)
(B)
(C)
与
相交但不垂直 (D)不能确定，与字母取值有关
6．(训练题28)已知
展开式中的实部是关于
的多项式，则此多项式的和为(B)．
(A)
(B)0 (C)
(D)
二、填空题（本题满分54分，每小题9分）
1．(训练题28)已知
．则
1 ．
2．(训练题28)不等式
的解的集合为 
．
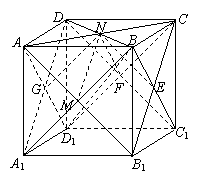
3．(训练题28)如图2，直三棱柱
中，底面是等腰直角三角形，
，
，
，连
，则平面
与平面
所成二角面的平面角为 
（用反三角函数表示）．
4．(训练题28)已知
，则
10 ．
5．(训练题28)已知
．则
0 
．
6．(训练题28)有五个匣子，每个匣子有一把钥匙，并且钥匙不能通用．如果随意在每个匣子内放入一把钥匙，然后把匣子全部锁上，现允许砸开一个匣子，使得能相继用钥匙打开其余4个匣子，那么钥匙的放法有 24 种．
三、(训练题28)(本题满分20分)已知直线
与轴交于
点，与
轴交于
点，且与椭圆
没有公共点．求证：
．
四、(训练题28)(本题满分20分)如图３，在棱长为的正方体
中，沿
切去它的两角，再沿面
切去两角．求所剩下几何体的体积．
五、(训练题28)(本题满分20分)已知
为等差数列，
，求证：
．
第二试
一、(训练题28)(本题满分50分)梯形
中，
与
均为锐角，连对角线
，求证：必可把
分成4个互不重叠的三角形
，把
也分成4个互不重叠的三角形
，使得
．
二、(训练题28)(本题满分50分)已知数列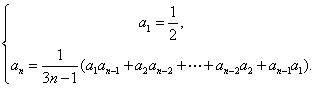
求证：
．
三、(训练题28)(本题满分50分)凸66边型内角中，必存在两个角
，使得
．