数学奥林匹克高中训练题（26）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题59)已知
是两个不等的正数，则
，
，
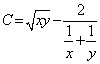的大小顺序是(C)．
(A)
(B)
(C)
(D)
2．(训练题59)函数
与
有相同的定义域，对定义域中任何
，有
，
，且当
时，
，则
是(B)．
(A)奇函数 (B)偶函数 (C)既是奇函数又是偶函数 (D)非奇非偶函数
3．(训练题59)已知
为非零常数，若
， 
，则对任意的
(C)．
(A)
(B)
(C)仅当
时， (D)仅当
时
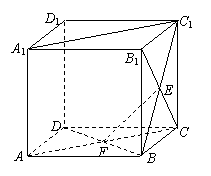4．(训练题59)如图1，在棱长为
的正方体
中，点E、F分别是面
和
的中心，则异面直线
与
的距离为(C)．
(A)
(B)
(C)
(D)
5．(训练题59)已知周期数列
满足
，若
，则当该数列的周期最小时，数列的前2002项的和是(B)．
(A)2002 (B)1335 (C)1949 (D)1428
6．(训练题59)设点
分别为椭圆
的左右两焦点，
为右准线，若在椭圆上存在点
，使
，点到的距离
成等比数列，则椭圆离心率
的取值范围是(A)．
(A)
(B)
(C)
(D)
二、填空题（本题满分54分，每小题9分）
1．(训练题59)已知复数
，满足
，则
．
2．(训练题59)已知
，设
，则
的取值范围是 
．
3．(训练题59)已知在三棱锥
中，底面三角形每个顶点处的三个面角和均为
，底面三角形三边分别是
、
和
，则该三棱锥的体积是 
．
4．(训练题59)设
，定义
，且
，则
．
5．(训练题59)已知焦点在轴上的椭圆
，点
是过原点的直线与椭圆的两个交点，若数
使得在椭圆上还存在另一点
，使
为正三角形，则对所有这样的，的面积最大值是 
．
6．(训练题59)已知方程组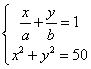
，有且仅有整数解，则满足题意的实数对
的个数是 60 ．
三、(训练题59)(本题满分20分)已知
，且
，求证：
．
四、(训练题59)(本题满分20分)给定空间不共面的
个点
．试问：是否一定存在这样一个平面，仅过这个点的其中三个？并请证明你的结论．
五、(训练题59)(本题满分20分)如果在一条平面曲线上存在四点，使得这四点构成的图形是一个菱形，则称该曲线存在内接菱形．现已知双曲线
，双曲线
，其中
．证明：在双曲线
与
中有且仅有一条存在内接菱形．
第二试
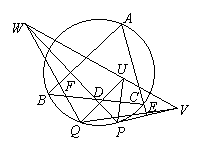
一、(训练题59)(本题满分50分)如图2，点
是的外接圆上（异于
）的两点，点
关于直线
的对称点分别是
，连线
分别与直线交于
，求证：（1）三点共线；（2）三点共线．
二、(训练题59)(本题满分50分)已知
，且
，试求
的最大值和最小值．
三、(训练题59)(本题满分50分)已知
是自然数
的一个排列，且满足：对任意
，均有
．(1)若记
为数
在排列中所处位置的序号（如排列
中，
）．求证：对每一个满足题意的排列，均有
成立．(2)试求满足题意的排列的个数
．