上学期高三数学期中考试
一、选择题：本小题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知函数y=2x (x∈R)的数值域为集合M，函数y=x2(x∈R)的值域为集合N，则
( )
(A) M∩N={2,4} (B) M∩N={4,16}
(C) M=N
(D) M
N
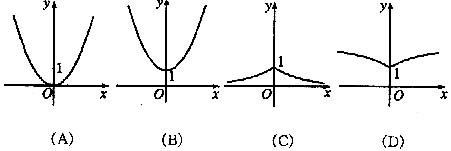
2.函数y=aX(0<a<1)的图像是 ( )
3.成等差数列的3个正数的和等于15,并且这三个数分别加上1,3,9后又成等比数例.
那么这三个数的乘积等于 ( )
(A) 210 (B) 105
(C )70 (D) 35
4.不等式
≤x－1的解集是
( )
(A) (－∞,－
∪
(B) 
∪
(C) [－1,3]
(D) ( －∞,－3) ∪
5.若a, b∈R则“a>b”的一个充分必要条件是 ( )
(A)(a-b)(a2-ab+b2)>0 (B) a2>b2
(C) 
> 
(D)
lna>lnb
6.定义在R上的偶函数f(x)满足f(x+4)=－f(x),且在[0,4]上是减函数,则 ( )
(A) f(10)<f(13)<f(15) (B) f(13)<f(10)<f(15)
(C) f(15)<f(10)<f(13) (D) f(15)<f(13)<f(10)
7.设函数f(x)= －1(x<0)
0 (x=0) ,则
(a≠b)的值应为( )
1 (x>0)
(A) a (B) b
( C) a, b之中较少的数 (D) a, b 之中较大的数
8.已知f(x)=log2x, 若f(a)>f(2.5),则a的取值范围是 ( )
(A) (0,
) ∪ (1, 
) (B) (
,+∞)
(C) (0, )∪( ,+∞)
(D) (,)
二、填空题：本大题共6小题，每小题5分。共30分。把答案填在题中横线上。
9.若f(x)=x2-1(x≤－2),则f－1(4)=___________.
10.已知z1=2+3i, z2=5-i那么 z1-z2 =_________;
又若f(z)=1－
，那么f(
－
)=__________
11.已知x∈（0，），则当x=____________时,x(5－2x)的最大值是_________.
|
=____________
13.有一组数据：x1，x2 ,…xn (x1≤x2≤…≤xn) ,它们的算术平均值为10，若去掉其中最大的xn,余下数据的算术平均值为9；若去掉其中最小的x1,余下数据的算术平均值为xn,余下的算术平均值为11. 则
x1关于n的表达式为_________; xn关于n的表达式为___________.
14.从3男7女共10个人中选出5人
若其中甲、乙两人必选在内，共有_________种不同的选法,(用数字作答)
若至少一名男生被选在内,共有________种不同的选法.(用数字作答)
三、解答题：本大题共6个小题，共80分。解答应写出文字说明、证明过程或演算步骤。
15.(本小题满分14分)
(理科学生作) 解关于x的不等式
>logax-3 其中0<a<1
(文科学生作)
解不等式
>
16.(本小题满分12分)
已知复数z满足z· +2i=3+ai 其中a是实数
（Ⅰ）求复数z（写关于a的表达式）
（Ⅱ）当实数a为何值时，满足条件的复数z存在？
17.(本小题满分14分)
已知一次函数y=f(x)满足f(0)=1,又点An(n,
) (n=1,2,3…)在这个一次函数y=f(x)
的图象上,若a1=1,且当n≥2时,恒有－
=1
（Ⅰ）求f(x)的解析式:
(Ⅱ)分别写出a2, a3, a4的值,并求出数列{an}的的通项公式.请予以证明.
18.(本小题满分12分)
经市场调查分析知,某地明年从年初开始的前n个月,对某种商品需求总量f(n)(万件)
近似地满足下列关系:f(n)=
(n+1)(35－2n)
(n=1,2,3,…12)
(Ⅰ)写出明年第n个月这种商品需求量g(n) (万件)与月份n的函数关系式,并求出哪几个月的需求量超过1.4万件;
(Ⅱ)若计划每月该商品的市场投放量都是p 万件,并且要保证每月都满足市场需求,则p至少为多少万件?
19.(本小题满分16分)
已知 数列{an}中,a1>0,且an+1－
.
(Ⅰ)试求a1的值,使得数列{an}是一个常数数列;
(Ⅱ)试求a1的取值范围,使得an+1>an 对任何自然数n都成立;
(Ⅲ)若a1=4,设bn= an+1－an(n=1,2,3…),并以Sn表示数列{bn}的前n项的和,试证明:Sn<.
20. (本小题满分12分)
(理科学生作)已知 二次函数f(x)=x2+ax+b (a,b ∈R)的定义域为[-1,1],且f(x)的最大值为M.
(Ⅰ)试证明1+b≤M;
(Ⅱ)试证明M≥
;
(Ⅲ)当M=时,试求出f(x)的解析式.
(文科学生作)设二次函数f(x)=ax2+bx+c (a,b,c∈R)
若x1<x2<x3<x4且x1+x4=x2+x3
(Ⅰ)试证 f(x1)+f(x4)=f(x1+x4)－2ax1·x4+c
(Ⅱ)试比较 x1·x4与x2·x3之间的大小关系.
(Ⅲ)试比较 f(x1)+f(x4)与f(x2)+f(x3)之间的大小关系.
上学期高三数学期中考试答案
2003·11
一、选择题（每小题5分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 |
| 答案 | D | C | B | B | A | B | D | C |
二、填空题（每小题5分，若有两空时，其中第一空3分，每二空2分.共30分.）
9.－
10.5；4－4i
11.
；
12. 1(0<q≤1) 13.
11－n；n+9
(q>1)
14.56；231
三、解答题（共80分）
15.(本小题满分14分)
解：设：logax=t,代入原不等式得
>t-3(*)…………………………3分
上述不等式
(Ⅰ) t－3≥0
t－1≥0
或(Ⅱ) t-3<0
t-1>(t-3)2
t-1 ≥ 0 ………………………………8分
又由(Ⅰ) t≥3
(t-2)(t-5)<0 解得3≤t<5
由（Ⅱ）解得1≤t<3
∴不等式（*）的解集为{t1≤t<3或3≤t<5},
即{t1≤t<5}………………………………………………12 分
（理科评分）∴1≤logax<5∵0<a<1, ∴a5<x≤a
即原不等式的解集为{xa5<x≤a}.…………………………………14 分
(文科评分) ∴1≤log
x<5 
<x≤
即原不等式的解集为{x<x≤}.…………………………………14分
16.(本大题满分12分)
解: (Ⅰ)设,z=x+yi (x,y∈R),则=x－y i…………………2 分
代入题设 z·+2i=3+ai(a∈R)
得：(x+yi)·(x- yi)+2i(x- yi)=3+ ai……………………………4分
整理后,由复数相等的定义得方程组:
x2+y2+2y=3
2x=a ………………………………………………6分
y2+2y+
－3=0………………………………………………8分
可得：z=
+
i…………………………………10分
(Ⅱ)∵y∈R,∴△=4－4·(－3)≥
解出 －4≤a≤4…………………………………………………12分
17.(本大题满分14分)
解：(Ⅰ)设y=f(x)=kx+b, ∵f(0)=1
∴b=1………………………………………………………………3 分
又An在y=f(x)的图像上,
∴=kn+1，又 －=k(n－1)+1,
而由－=kn+1－k(n－1)－1=1
∴k=1……………………………………………6分
∴f(x)=x+1
(Ⅱ)∵=n+1,a1=1,
当n=1时,由
=2,得a2=1×2
当n=2时,由
=3,得a3=1×2×3
当n=3时,由
=4,得a4=1×2×3×4………………………………………7分
猜想：an=n!……………………………………………………9分
下面数学归纳法证明；
(1) 当n=1时,结论正确;
(2) 假设当n=k(1≤k≤n)时结论成立,即ak=k!
则当n=k+1时,
ak+1=ak·(k+1)=k !·(k+1)=(k+1)!结论亦正确
由(1)、(2)可知原式an=n!对任何n∈N都成立，…………………………14分
18.(本小题满分12分)
解：当n=1时,g(1)=f(1)=
………………………………2分
当n≥2时,
g(n)=f(n)－f (n－1)=
(－n2+12n)
(经检验对n=1也成立)
∴g(n)= (－n2+12n) (n∈N)……………………………5分
解不等式(－n2+12n)>1.4得5<n<7
∵n∈N, ∴n=6.
即第6个月的需求量超过1.4万件.……………………………7分
(Ⅱ)由题设可知,对于n=1,2,…,12恒有:np≥f(n),
即p≥
(n+1)·(35－2n)……………………………………………9分
=[－2(n－
)2+
+35]
当且仅当n=8时,pmin=
=1.14
∴每月至少投放1.14万件.………………………………………………12分
19.(本题满分16分)
解：(Ⅰ)欲使数列{an}是一个常数数列,则
an+1==an,………………………………………2分
又依a1>0，可以推得an>0并解出：an=
即a1=an=………………………………………………………4分
(Ⅱ)研究an+1-an=-
=
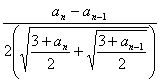(n≥2)…………………6分
注意到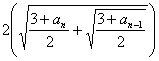
>0
因此,可以得出：an+1－an , an－an-1 , an-1－an-2,…a2-a1有相同的符号.………………………………8分
要使an+1>an对任意自然数都成立,只须a2-a1>0即可.
由
>0,解得：0<a1<.………………………………10分
(Ⅲ)用与(Ⅱ)中相同的方法,可得
当a1>时,an+1<an对任何自然数n都成立.
因此当a1=4时,an+1-an<0………………………………12分
∴Sn=b1+b2+…bn
=a2-a1+a3-a2+…+an+1-an
=a1-a2+a2-a3+…+an-an+1
=a1-an+1=4-an+1…………………………………14分
又：an+2< an+1=4－an+1
可得an+1>,故Sn<4－=………………………………16分
20.(本大题满分12分)
(理科评分)(Ⅰ)证明:
∵M≥f(-1)=1-a+b
M≥f(1)=1+a+b…………………………2分
2M≥1-a+b+1+a+b
≥(1-a+b)+(1+a+b)=2(1+b)
=11+b……………………4分
∴M≥
(Ⅱ)证明:依题意,M≥f(-1), M≥f(0), M≥f(1)
又f(-1)=1-a+b
f(1)=1+a+b
f(0)=b………………………………………………5分
∴4M≥f(-1)+2f(0)+f(1)…………………………7分
=1-a+b+2b+1+a+b
≥(1-a+b)-2b+(1+a+b)=2……………………10分
∴M≥
(Ⅲ)解:依M=时,f(0)=b≤ －≤b≤①
同理－≤1+a+b≤
②
－≤1－a+b≤
③
②+③得：－≤b≤－
由b=－时,分别代入②、③,得： －1≤a≤0
0≤a≤1
∴a=0
因此,f(x)=x2－…………………………12分
(文科评分)
解：(Ⅰ)f(x1)+f(x4)=a(x12+x42)+b(x1+x4)+2c
=a(x1+x4)2－2ax1·x4+b(x1+x4)+2c……………2分
=f(x1+x4)－2ax1 x4+c……………………4分
(Ⅱ)令 x1+x4=x2+x3=u 则x4=u－x1,x3=u－x2
研究：x2·x3－x1·x4=x2(u－x2)－x1(u－x1)
=(x1－x2)(x1+x2－u)
=(x1－x2)(x1－x3)>0
这全由于x1<x2<x3的缘故.…………………………8分
所以x2x3>x1x4
(Ⅲ)研究[f(x1)+f(x4)]－[f(x2)+f(x3)]
=[f(x1+x4)－2ax1x4+c]－[f(x2+x3)－2ax2x3+c]
=2a(x2x3－x1x4)………………………10分
因此 当a>0时, f(x1)+f(x4)>f(x2)+f(x3)
当a<0时, f(x1)+f(x4)< f(x2)+f(x3)……………12分
注:其它正确解法可按相应步聚给分.