数学奥林匹克高中训练题(18)
第一试
一、选择题(本题满分36分,每小题6分)
1.(训练题23)![]() 除以
除以![]() 所得的余数是(D).
所得的余数是(D).
(A) ![]() (B)
(B) ![]() (C) 1996 (D)
(C) 1996 (D) ![]()
2.(训练题23)若在抛物线![]() 的上方可作一个半径为
的上方可作一个半径为![]() 的圆与抛物线相切于原点
的圆与抛物线相切于原点![]() ,且该圆与抛物线没有别的公共点,则
,且该圆与抛物线没有别的公共点,则![]() 的最大值是(A).
的最大值是(A).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.(训练题23)考虑某长方体的三个两两相邻的面上的三条对角线及体对角线(共四条线段),则正确的命题是(B).
(A)必有某三条线段不能组成一个三角形的三边.
(B)任何三条线段都可组成一个三角形,其中每个内角都是锐角.
(C)任何三条线段都可组成一个三角形,其中必有一个是钝角三角形.
(D)任何三条线段都可组成一个三角形,其形状是“锐角的”或者是“非锐角的”,随长方体的长,宽,高而变化,不能确定.
4.(训练题23)若![]() ,则
,则![]() 的取值范围是(D).
的取值范围是(D).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.(训练题23)有5个男孩与3个女孩站成一排照相任何两个女孩都不相邻,则其可能的排法个数是(A).
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
6.(训练题23)使得![]() 成立的最小正整数
成立的最小正整数![]() 是(B).
是(B).
(A)4 (B)5 (C)6 (D)7
二、填空题(本题满分54分,每小题9分)
1.(训练题23)设![]() ,若函数
,若函数![]() 关于直线
关于直线![]() 对称,且
对称,且![]() 与
与![]() 有公共点,则
有公共点,则![]() 的取值范围是
的取值范围是 ![]() .
.
2.(训练题23)设![]() 且存在
且存在![]() ,适合
,适合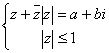 则
则![]() 的最大值等于
的最大值等于 ![]() .
.
3.(训练题23)设![]() ,若
,若![]() ,则
,则![]() 等于
等于 ![]() .
.
4.(训练题23)设![]() 是棱长为1的正方体,则上底面
是棱长为1的正方体,则上底面![]() 的内切圆上的点
的内切圆上的点![]() 与过顶点
与过顶点![]() 的圆上的点
的圆上的点![]() 之间的最小距离
之间的最小距离![]()
![]() .
.
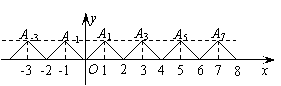 5.(训练题23)如图,在直角坐标系
5.(训练题23)如图,在直角坐标系![]() 中,有一条周期性折线(函数)
中,有一条周期性折线(函数)![]() 现把该曲线绕原点
现把该曲线绕原点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到另一条曲线
得到另一条曲线![]() ,则这两条曲线与
,则这两条曲线与![]() 轴及直线
轴及直线![]() 围成的图形的面积等于
围成的图形的面积等于 ![]() .
.
6.(训练题23)设![]() 都是正整数,且
都是正整数,且![]() 则
则![]() 的个位数等于
4
.
的个位数等于
4
.
第二试
一、(训练题23)(本题满分25分) 求证:在复平面上,点集![]() 中,除去某一个点外的所有的点都在圆环
中,除去某一个点外的所有的点都在圆环![]() 中.
中.
二、(训练题23)(本题满分25分)已知抛物线![]() 其焦点为
其焦点为![]() .试问:是否存在过
.试问:是否存在过![]() 点的弦
点的弦![]() (
(![]() 均在抛物线上,且
均在抛物线上,且![]() 在第一象限内),以及
在第一象限内),以及![]() )轴正半轴上的一点
)轴正半轴上的一点![]() ,使得
,使得![]() 三点构成一个以
三点构成一个以![]() 为直角顶点的等腰直角三角形?证实你的回答.如果回答是肯定的,请求出直线
为直角顶点的等腰直角三角形?证实你的回答.如果回答是肯定的,请求出直线![]() 的方程.
的方程.![]()
|
四、(训练题23)(本题满分35分)设![]() ,
,![]() ,且
,且![]() 又存在
又存在![]() 使得当
使得当![]() 时有
时有![]() ,当
,当![]() 时,有
时,有![]() .求证:
.求证:![]() .
.