数列应用题中的递推关系-高中三年级数学试题练习、期中期末试卷、测验题、复习资料-高中数学试卷-试卷下载

数列应用题中的递推关系

以数列知识作为背景的应用题是高中应用题中的常见题型，要正确快速地求解这类问题，需要在理解题意的基础上，正确处理数列中的递推关系。

一、等差、等比数列问题

等差、等比数列是数列中的基础，若能转化成一个等差、等比数列问题，则可以利用等差、等比数列的有关性质求解。

例1、流行性感冒（简称流感）是由流感病毒引起的急性呼吸道传染病。某市去年11月份曾发生流感，据资料记载，11月1日，该市新的流感病毒感染者有20人，以后，每天的新感染者平均比前一天的新感染者增加50人。由于该市医疗部门采取措施，使该种病毒的传播得到控制，从某天起，每天的新感染者平均比前一天的新感染者减少30人，到11月30日止，该市在这30天内感染该病毒的患者共有8670人，问11月几日，该市感染此病毒的新患者人数最多？并求这一天的新患者人数。

分析：设11月n日这一天新感染者最多，则由题意可知从11月1日到n日，每天新感染者人数构成一等差数列；从n+1日到30日，每天新感染者构成另一个等差数列。这两个等差数列的和即为这个月总的感染人数。

略解：由题意，11月1日到n日，每天新感染者人数构成一等差数列a_n，a₁=20,d₁=50,11月n日新感染者人数a_n=50n—30；从n+1日到30日，每天新感染者人数构成等差数列b_n,b₁=50n-60,d₂=—30，b_n=(50n-60)+(n-1)(-30)=20n-30,11月30日新感染者人数为b_30-n=20(30-n)-30=-20n+570.

故共感染者人数为：=8670，化简得：n²-61n+588=0,解得n=12或n=49(舍)，即11月12日这一天感染者人数最多，为570人。

二、a_n- a_n-1=f(n),f(n)为等差或等比数列

有的应用题中的数列递推关系，a_n与a_n-1的差（或商）不是一个常数，但是所得的差f(n)本身构成一个等差或等比数列，这在一定程度上增加了递推的难度。

例2、某产品具有一定的时效性，在这个时效期内，由市场调查可知，在不作广告宣传且每件获利a元的前提下，可卖出b件。若作广告宣传，广告费为n千元时比广告费为（n-1）千元时多卖出件，（n∈N^*）。

（1）试写出销售量s与n的函数关系式；

（2）当a=10,b=4000时厂家应生产多少件这种产品，做几千元广告，才能获利最大？

分析：对于(1)中的函数关系，设广告费为n千元时的销量为s_n,则s_n-1表示广告费为(n-1)元时的销量，由题意，s_n_——s_n-1=，可知数列{s_n}不成等差也不成等比数列，但是两者的差构成等比数列，对于这类问题一般有以下两种方法求解：

解法一、直接列式：由题，s=b++++…+=b(2-)

（广告费为1千元时，s=b+；2千元时，s=b++；…n千元时s=b++++…+）

解法二、（累差叠加法）设s₀表示广告费为0千元时的销售量，

由题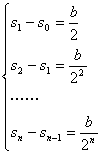：，相加得S_n-S₀=+++…+,

即s=b++++…+=b(2-)。

（2）b=4000时，s=4000(2-),设获利为t,则有t=s·10-1000n=40000(2-)-1000n

欲使T_n最大，则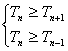：，得，故n=5,此时s=7875。

即该厂家应生产7875件产品，做5千元的广告，能使获利最大。

三、a_n= C·a_n-1+B，其中B、C为非零常数且C≠1

例3、某企业投资1千万元于一个高科技项目，每年可获利25%，由于企业间竞争激烈，每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入，方能保持原有的利润增长率，问经过多少年后，该项目的资金可以达到或超过翻两番（4倍）的目标？（lg2=0.3）。

分析：设经过n年后，该项目的资金为a_n万元，则容易得到前后两年a_n和a_n-1之间的递推关系：a_n =a_n-1（1+25%）-200（n≥2），对于这类问题的具体求解，一般可利用“待定系数法”：

解：由题，a_n =a_n-1（1+25%）-200（n≥2），即a_n =a_n-1-200，设a_n +λ=（a_n-1+λ），展开得a_n =a_n-1+λ，λ=-200，λ=-800，∴a_n -800=（a_n-1-800），即{a_n -800}成一个等比数列，a₁=1000(1+25%)-200=1050, a₁-800=250，∴a_n -800=250（）^n-1，a_n =250（）^n-1+800，令a_n≥4000，得（）ⁿ≥16，解得n≥12,即至少要过12年才能达到目标。