全国高中数学联赛模拟试题(一)
第一试
一、选择题(共36分)
1.
在复平面上，非零复数z1，z2在以z=i对应的点为圆心，1为半径的圆上，
的实部为零，argz1＝，则z2＝
( )
A.－i B.i C.－i D.i
2.
已知函数f(x)＝loga(ax2－x＋)在[1，2]上恒正，则实数a的取值范围是( )
A.() B.(，＋∞) C.(，＋∞) D.(，＋∞)
3.
已知双曲线过点M(－2，4)和N(4，4)，它的一个焦点为F1(1，0)，则另一个焦点F2的轨迹方程是 ( )
A.＝1(y≠0)或x＝1(y≠0)
B.＝1(x≠0)或x＝1(y≠0)
C.＝1(y≠0)或y＝1(x≠0)
D.＝1(x≠0)或y＝1(x≠0)
4.
已知正实数a，b满足a＋b＝1，则M＝的整数部分是 ( )
A.1 B.2 C.3 D.4
5.
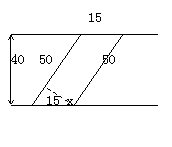
一条笔直的大街宽度为40米，一条人行横道穿过这条街，并与街道成一定的角度，人行横道长度为50米，与大街边缘结合部的宽度为15米，则人行横道的宽度为( )
A.9米 B.10米 C.12米 D.15米
6.
一条铁路原有m个车站，为适应客运需要新增加n(n＞1)个车站，结果客运车票增加了58种(注：从甲站到乙站和从乙站到甲站需要两种不同的车票)，那么原有车站的个数为
A.12 B.13 C.14 D.15 ( )
二、填空题(共54分)
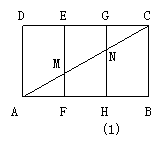
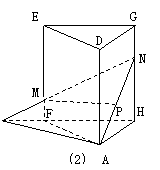
7. 长方形ABCD的长AB是宽BC的2倍，把它折成无底的正三棱柱，使AD与BC重合，折痕线EF，GH分别交原来长方形对角线AC于M、N，则折后截面AMN与底面AFH所成的角是_____.
8. 在△ABC中，a，b，c是角A，B，C的对边，且满足a2＋b2＝2c2，则角C的最大值是_____.
9. 从盛满a升(a＞1)纯酒精的容器中倒出1升，然后加水填满，在倒出1升混合溶液后又加水填满，如此继续下去，则第n次操作后溶液的浓度为__________________.
10. 已知函数f(x)和g(x)的定义域均为非负实数集，对任意的x≥0，规定f(x)*g(x)＝min{f(x)，g(x)}，若f(x)＝3－x，g(x)＝，则f(x)*g(x)的最大值是_________.
11. 从1到100的自然数中，每次取出不同的两个数，使它们的和大于100，则可有_______种不同的取法.
12. 若实数a＞0，则满足a5－a3＋a＝2的a值属于区间:①(0，)；②()，③(，＋∞)；④(0，).其中正确的是_________________.
三、解答题(共计60分)
13. (20分)求证：经过正方体中心的任意截面的面积不小于正方体一个侧面的面积.
14. (20分)直线Ax＋By＋C＝0(ABC≠0)与椭圆b2x2＋a2y2＝a2b2相交于P和Q两点，O为坐标原点，且OP⊥OQ，求证：.
15. (20分)某新建商场设有百货部、服装部和家电部三个经营部，共有190名售货员，计划全商场的日营业额(每日卖出商品所收到的总金额)为60万元，根据经验，各部商品每1万元营业额需要售货员人数及每1万元营业额所得利润情况如表所示，商场将计划日营业额分配给三个经营部，同时适当安排各部的营业员人数，若商场预计每日的总利润为c万元，且19≤c≤19.7，又已知商场分配给经营部的营业额均为整数万元，问这个商场怎样分配营业额给三个部？各部分别安排多少名营业员？
| 部门 | 每1万元营业额需要售货员人数 | 每1万元营业额所得利润(万元) |
| 百货部 | 5 | 0.3 |
| 服装部 | 4 | 0.5 |
| 家电部 | 2 | 0.2 |
第二试
一、(50分)矩形ABCD的边AD＝λ·AB，以AB为直径在矩形外作半圆，在半圆上任取不同于A、B的一点P，连PC、PD交AB于E、F，若AE2＋BF2＝AB2，求正实数λ的值.
二、(50分)若ai∈R＋(i＝1，2，……，n)，S＝
，且2≤n∈N，求证：
.
三、(50分)无穷数列{cn}由下列法则定义：cn＋1＝1－1－2cn，而0≤c1≤1
(1)证明：仅当c1是有理数时，数列自某一项开始成为周期数列；
(2)存在多少个不同的c1值，使得数列自某项之后以T为周期(对于每个T＝2，3，……)?
全国高中数学联赛模拟试题(一)
参考答案
第一试
一、选择题
1. A
如图所示，设复数z1对应的点为Z1，则
OZ1＝2sin＝1，∴
z1＝i
再设z2＝x＋yi(x，y∈R)
由z2－i＝1得x2＋(y－1)2＝1 …………①
∵ (i)(x＋yi)的实部等于0，
∴ x＋y＝0
…………②
联立①②解得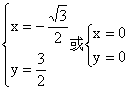
(舍去)
故z2＝－i
2. C
设g(x)＝ax2－x＋，首先由g(x)＞0得
a＞
当1≤x≤2时，(－
从而a＞，在此前提下，易知函数g(x)＝ax2－x＋的对称轴x＝在区间[1，2]的左边，
从而g(x)在[1，2]上是增函数.
当a＞1时，f(x)在[1，2]上是增函数，有
f(1)＝loga(a－1＋)＞0，Þ a＞
当＜a＜1时，f(x)在[1，2]上是减函数，有
f(2)＝loga(4a－2＋)＞0，Þ
综上：或a＞
3. A
易知MF1＝NF1＝5
而MF1－MF2＝NF1－NF2 即5－MF2＝5－NF2
当5－MF2＝5－NF2时，即MF2＝NF2时，点F2的轨迹是线段MN的中垂线，
其方程为x＝1(y≠0)
当5－MF2＝NF2－5时，即MF2＋NF2＝10时，点F2的轨迹是以M、N为焦点，长轴长为10的椭圆，其方程为＝1(y≠0)
4. 
B
一方面，M＞＝2
另一方面，M＜＝1＋a＋1＋b＝2＋(a＋b)＝3
所以，2＜M＜3
5. C
如图，人行横道的面积S＝15×14＝600
∴ S＝50x＝600 Þ x＝12
6. C
新增的n个车站之间需要Pn2种车票，新增的n个车站与原来的m个车站之间需要2mn种车票，从而Pn2＋2mn＝58，即n(n－1＋2m)＝58
注意到n和n－1＋2m都是整数，而58只能分解为1×58和2×29两种情况，又n＞1
所以n＝2，n－1＋2m＝29，或n＝29，n－1＋2m＝2，或n＝58，n－1＋2m＝1
只有第一组有满足题意的解：n＝2，m＝14
二、填空题
7.；
折叠后，仍然有AF＝FH＝HB(或HA，折叠后A点和B点重合)
AM＝MN＝NC，且它们的长度没有变，仍然等于折叠前的长度，但对角线AC由直线段变成了折线段，A、M、N三点由原来共线变成了A、M、N三点构成三角形.
设AD＝a，则AB＝2a，图(1)为折叠前的长方形，有AC＝a，AM＝MN＝a，AF＝FH＝HB＝a，MF＝，HN＝.
设平面AMN与平面AFH的夹角为θ(图(2))，由S△AFH＝a2.
在Rt△NHA中，AN＝
取AN的中点P，∵ AM＝MN Þ MP⊥AN
在Rt△MPA中，MP＝＝a
∴ S△AMN＝
∴ cosθ＝
8.；
∵ a2＋b2＝2c2，∴ cosC＝
∴ a2－4abcosθ＋b2＝0
即()2－(4cosC)＋1＝0(∵
b≠0)
因为是正实数，所以4cosC＞0且△≥0
解得：cosC≥，所以C≤
9.(1－)n；
开始浓度为1，操作一次后溶液浓度为a1＝1－，
设操作n此后的溶液浓度为an，则操作n＋1次后溶液的浓度为an＋1＝an(1－)
∴ {an}是首项、公比均为1－的等比数列，∴ an＝a1qn－1＝(1－)n
10.2－1；
∵ x≥0，令3－x＞，解得0≤x≤4－2
所以f(x)*g(x)＝
∵ 3－x在R上单调递减，故当x≥4－2时，
f(x)*g(x)≤f(4－2)*g(4－2)＝3－(4－2)＝2－1
当0≤x＜4－2时，单调递增，故当x∈[0，4－2)时，
f(x)*g(x)＜－1
综上所知，f(x)*g(x)的最大值为2－1
11.2500；
以1为被加数，则1＋100＞100，有1种取法，
以2为被加数，则2＋100＞100，2＋99＞100，有2种取法，
依次可得，被加数为n(n∈N，n≤50)时，有n种取法，
但51为被加数时，要扣除前面已取过的情况，只能取52，53，……，100，有49种取法，
同理，被加数为52时，有48种取法，
依次可得，当被加数为n(n∈N，51≤n≤100)时，分别有100－n种取法，
所以，不同的取法共有(1＋2＋3＋……＋50)＋(49＋48＋……＋1)＝2500种
12.③④
∵ a6＋1＝(a2＋1)(a4－a2＋1)＝(a5－a3＋a)＝2(a＋)，(a≠0)
∵ a＞0且a≠1，∴ a6＋1＞4，∴ a6＞3，即a＞
又a5－a3＋a＝2，∴ ＋1＝a2＋＞2
∴ a3＜2，即a＜，综合可知，应填③④
三、
13．显然，所作截面是一个中心对称的凸多边形，它是一个四边形或六边形.
如果截面是一个四边形，那么它一定没有截到立方体的某一组对面，其面积不小于这组对面中的一个，命题成立.
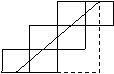
如果截面是一个六边形，那么它一定截到了正方体的六个面，将立方体展开在一个平面上，如图，设界面的周长为l，正方体的棱长为a，则 l≥AB＝a
由于正方体的中心是内切球的球心，所以截面内含有半径为的圆，从而有
S截面≥a2＞a2
14．将Ax＋By＋C＝0变形为1＝－，代入椭圆方程，得
b2x2＋a2y2＝a2b2(－)2
整理得：(a2b2B2－a2C2)y2＋2ABa2b2xy＋(a2b2A2－b2C2)x2＝0
当x＝0时，显然成立；
当x≠0时，同除以x2得：
(a2b2B2－a2C2)()2＋2ABa2b2()＋(a2b2A2－b2C2)＝0
该方程的两根为OP，OQ的斜率，
∵ OP⊥OQ，所以－1＝，即
15．设分配给百货、服装、家电营业额分别为x，y，z(万元)，(x，y，z是正整数)，则
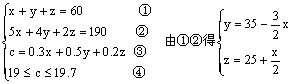
所以c＝0.3＋0.5(35－)＋0.2(25＋)＝22.5－0.35x
代入④得8≤x≤10，∵ x，y，z必为正整数，
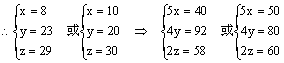
第二试
一、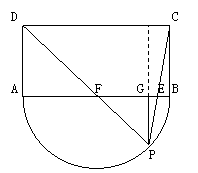
如图，过P点作PG⊥AB，垂足为G，不失一般性，设AB＝2，则AD＝2λ
再设PG＝h，∠PDA＝α，PCB＝β，
则AE＝AB－BE＝2－2λtanβ
BF＝AB－AF＝2－2λtanα
∵ (2λ＋h)tanα＋(2λ＋h)tanβ＝2
∴ tanα＋tanβ＝ ……①
又(2λ＋h)tanα(2λ＋h)tanβ＝h2
∴ tanαtanβ＝ ……②
∵ AE2＋BF2＝(2－2λtanα)2＋(2－2λtanβ)2＝AB2
∴ 8－8λ(tanα＋tanβ)＋4λ2(tan2α＋tan2β)＝4
即 λ2(tanα＋tanβ)2－2λ2tanαtanβ－2λ(tanα＋tanβ)＋1＝0
将①②代入上式，得
＋1＝0
∴ h2(1－2λ2)＝0
∵ h≠0，∴ 1－2λ2＝0，即λ＝
解法二：仍如上图，不失一般性，设AB＝2，则AD＝2λ，令AF＝x，BE＝y，
因为△PGE∽△CBE，于是
所以，GE＝
……………………①
同理，GF＝
……………………②
①＋②得：EF＝(x＋y)
即PG＝……………………③
由①②③得：GE＝·y
GF＝·x
∴ BG＝GE＋y＝
……………………④
同理AG＝
……………………⑤
又PG2＝AG·BG，综合③④⑤得
4λ2(
化简得：λ2(2－x－y)2＝xy ……………………⑥
又∵ AE2＋BF2＝AB2
∴ (2－x)2＋(2－y)2＝4
即 4－4(x＋y)＋x2＋y2＝0
∴ 2－2(x＋y)＋(x＋y)2＝2xy ……………………⑦
将⑥代入⑦得：
4－4(x＋y)＋(x＋y)2＝2λ2(2－x－y)2
即(2－x－y)2＝2λ2(2－x－y)2
∵ x＋y≠2，∴ 2λ2＝1，∴ λ＝
二、由柯西不等式，得
(S－ak)2≤(n－1)(
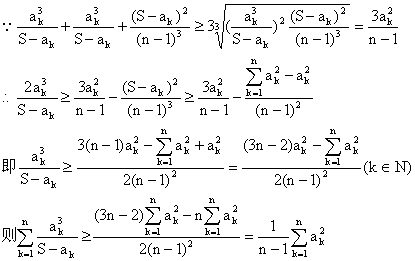
原不等式得证.
三、易知，题中的递推关系式即为
cn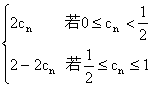＋1＝
…………①
(1)若C1为有理数，即c1＝，其中(p，q)＝1时，
对一切n，均有cn＝，其中pn∈{0，1，2，……，q}
故有n1＜n2，使得pn1＝pn2，从而cn1＝cn2，
于是由①式可知{cn}从第n1项之后呈周期变化.
假设数列自第n1项之后呈周期为T的变化，我们记：
cn1＝
，即用二进制表示cn1，其中ak＝0或1.
并记
＝1－ak，k∈N
……②
于是由①式可知
由此并结合归纳法，即知
由于cn1＋T＝cn1，故当a1＋……＋aT≡0(mod2)时，立即可得ak＝ak＋T，k∈N
由此表明cn1为二进制循环小数，故为有理数.
当a1＋……＋aT≡1(mod2)时，由于cn1＋T＝cn1，得ak＝
＝1－ak＋T，k∈N ……③
由于③式也表明ak＋T＝
，k∈N，所以
ak＝1－ak＋T＝1－＝1－(1－ak＋2T)＝ak＋2T，k∈N
故cn1也为有理数
再由递推式①知，cn1是由c1经过n1－1步有理运算得出的，所以，c1也必为有理数.
(2)如果分别取c1＝(0.
)2，c1＝(0.
)2，
……④
则可使{cn}分别以T＝2和T＝m，m≥3为周期，又易见，只要将c1取为④中的，k∈N，都可使数列最终以相应的T为周期，从而，对每个T＝2，3，……都有无穷多个c1使得数列自某项之后以T为周期变化.