【同步教育信息】
一. 本周教学内容：
三角、向量综合复习训练
【模拟试题】
一. 选择题（本大题共有12个小题，每小题5分，共60分。在每小题给出的四个选项只有一项是符合题目要求的）。
1. 函数
在
上的最小值是（ ）。
A. 
B. 
C. 
D. 
2. 已知
，则函数
的值域是（ ）。
A. 
B. 
C. 
D. 
3. 若
，且
、
满足关系式
，则
（ ）。
A. 
B. 
C. 
D. 
4. 使函数
为奇函数，且在
上是减函数的一个值是（ ）。
A. 
B. 
C. 
D. 
5. 如果
，那么
的值是（ ）。
A. 
或不存在 B. 或
C. D.
6. 函数
，
的最大值是
，则函数的值域是（ ）。
A.
B. 
C. 
D. 
7. 设向量
，那么与
平行的单位向量是（ ）。
A. 
或
B. 
C. 
或
D.
8. 已知
，
把
按向量
平移后得到一个新向量
，那么下面各向量中能与垂直的是（ ）。
A. 
B. 
C. 
D. 
9. 在 
中，
（ ）。
A. 
B. 
C. 
D. 
10. 设
、
、
是任意非零平面向量，且相互不共线，那么
①
②
③
④
若
，且三向量两两所夹角相等，则
中，是真命题的是（ ）。
A. ①② B. ②③ C. ③④ D. ①④
11. 把函数
的图象按向量平移后得到函数
的图象。则向量是（ ）。
A. 
B. 
C. 
D. 
12. 在
中，三内角
、
、
所对边长依次为
、
、
，且面积
，则角为（ ）。
A. 
B. 
C. 
D. 
二. 填空题（本大题共有4个小题，每小题4分，共16分。把答案填在题中横线上）。
13. 
。
14. 要得到函数
的图象，只要将函数
的图象
个单位长度。
15. 中三顶点坐标各是
、
、
。若把
边沿
边平移后得到线段
，
在边上，且
，则与
有交点
，那么线段
。
16. 在中，若三内角、、成等差数列，三边、、成等比数列，且
，则
。
三. 解答题（本大题共有6个小题，共74分。解答应写出文字说明，证明过程或演算步骤）。
17.（本小题满分10分）
求证：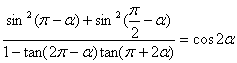
。
18.（本小题满分12分）
已知
，求
的值。
19.（本小题满分12分）
求函数
的最大值和最小值，并求出取最小值时
的值。
20.（本小题满分12分）
如图，是直角三角形，
，内角、、所对各边为、、。利用向量知识解答下列问题。
（1）若CD是斜边AB上的中线，证明
；
（2）若E是CD中点，连A、E并延长AE交BC于F，求AF的长度（用、表示）。
21.（本小题满分14分）
在海港A正东
处有一小岛B。现甲船从A港出发以
的速度驶向B岛。同时乙船以
的速度向北偏西的方向驶离B岛，不久之后，丙船则向正东方向从B岛驶出。当甲乙两船相距最近时，在乙船观测发现丙船在乙船南偏东方向。问此时甲丙两船相距多远？
22.（本小题满分14分）
如图，四边形ABCD的对角线AC和BD交于O，AO=OC，BO=OD，又以DC边的中心P为圆心，DP长为半径作⊙P。用向量知识解答下列问题：
（1）证明四边形ABCD是平行四边形；
（2）若⊙P的一直径MN两端可在圆周上滑动。问当直径MN在什么位置时，
取值最大？
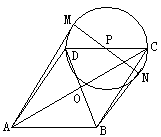
【试题答案】
一. 选择题
1. C 2. D 3. A 4. B 5. A 6. A
7. C 8. B 9. D 10. D 11. B 12. C
二. 填空题
13. 
14. 向左平行移动
15. 
16. 
三. 解答题
17.
证明：左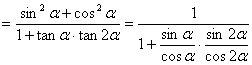边
右边。
∴ 原式成立。
18.
解：由已知得
，两边平方变形得
，
，
，即
。 ①
原式
把①代入，得：原式
。
另解：
把
代入得：
上式
。
19.
解：原解析式化为
。
设
，则
。
∴ 
。
∵ 
而
∴ 
时，有
；
时，有
。
令
，得
。
∴ 
。
函数
取最小值
时，的值应是
。
20.
（1）
证明：建立坐标系如图，设
，
，
，则由中点坐标公式得
，所以
，
∴
，即。
（2）
解：利用（1）及中点坐标公式得
。
设
，
则
，
，
因为
，（
为常数）
∴ 
∴ 
，
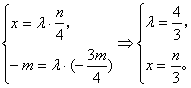
即
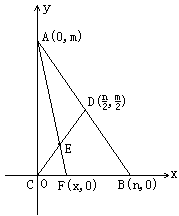
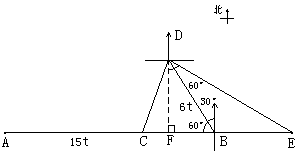
21.
解：作示意图如右，设在行驶
小时后，甲船到达C处，乙船到达D处，丙船到达E处。此时甲乙两船相距最近，依题意得：
。
∴ 当
时，
最小，即
取到最小值，也即甲乙两船相距最近。
又作
，则
，
，
∴ 
，
，
∴ 
为等腰三角形，
∴ 
∴ 
。
答：当甲乙两船相距最近时，甲丙两船相距21海里。
22.
（1）
证明：由已知得
，
，
则
即
。
所以
//且
。
∴ 四边形ABCD是平行四边形。
（2）
解：连接A、P、B、P则
。
设
，
的延长线与AB的延长线交于E，
，则
（
，
）
。
因为DP、PA、PB、AB长都是定值，所以当
即
时也即直径MN在与DC边重合的位置时，
取值最大。
