【同步教育信息】
一. 本周教学内容：
专题复习“三角函数与三角变形”
二. 重点与难点：
1. 三角函数的图象与性质；
2. 同角三角函数的基本关系式，诱导公式，和、差、倍、半角公式，和积互化公式等三角公式的应用。
三. 要点综述：
1. 三角函数是一类重要的初等函数，因其在复数（如复数的三角形式）解析几何（如直线的倾斜角，参数方程，极坐标），立体几何（如两条异面直线成角，直线与平面的成角，二面角）中有着广泛的应用，因此对三角函数与三角变形要有足够的认识。
2. 三角函数的周期性，以及y=sinx，y=cosx的有界性是试题经常考查的重要内容。要掌握形如y=Asin(ωx+
)或y=Acos(ωx+)的函数的周期的求法；灵活应用y=sinx，y=cosx的有界性研究某些类型的三角函数的最值（或值域）问题。
3. 三角恒等式的证明因其技巧性较强，一度成为数学的难点，近些年的高考试题对这类题目的考查在减少，要求有所降低，但我们应该充分重视三角变形，因为其中体现了对三角公式的运用能力，尤其体现了事物之间互相联系，互相转化的辩证思想。
4. 基于上述几点理由，建议同学们在复习这部分内容时，做到“立足课本，落实三基；重视基础，抓好常规”即复习时以中低档题目为主，注意求值化简题以及求取值范围的习题，另外，注意充分利用单位圆，三角函数图象研究问题。
【典型例题分析与解答】
例1. 
分析：
解：
例2.
求函数的最小值。
分析：若将sinx换元，则函数转化为二次函数，从而可把三角函数的最值问题转化为二次函数的最值问题，但要注意到：转化后所得二次函数的定义域。
解：
［注］在求解三角函数的最值时，注意三角函数的有界性。
例3. 
分析：一般地，要求三角函数的最小正周期，往往要用到如下结论：
式通过三角公式，变形为上述结论中的函数形式，于是：
或按如下方法化简解析式：
［注］一般地，如果给定的函数解析式不是形如y=Asin(ωx+)的形式，在求其最小正周期时，往往先将解析式变形为y=Asin(ωx+)的形式。
例4. 
分析一：由方程形式，可把该方程采取换元法，转化为二次函数：设sinx=t，则原方
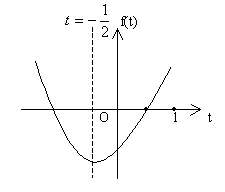
分析二：
解法如下：
例5. 
分析一：观察角，函数名称的关系后，易联想到万能公式，于是可以按照如下方式去求值。
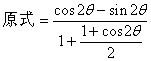
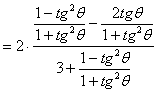
分析二：联想到关于sinθ，cosθ的齐次公式可以化切，于是可以按照如下方式求值。
［注］两相比较，发现，解法二更为简捷，事实上，对于已知tgθ的值，而求关于sinθ，cosθ的齐次公式的值时，方法二更具有通用性。
例6. 
分析：这是一道以三角形为背景材料的三角函数问题，要注意题中的隐藏条件：
的式子，从而立即求值。
解：
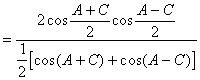
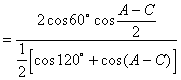
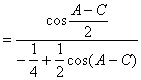
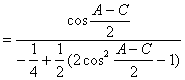
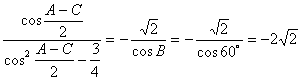
例7. 
解法一：
解法二：
例8. 
分析：对三角函数式化简的目标是：
（1）次数尽可能低；
（2）角尽可能少；
（3）三角函数名称尽可能统一；
（4）项数尽可能少。
观察欲化简的式子发现：
（1）次数为2（有降次的可能）；
（2）涉及的角有α、β、2α、2β，（需要把2α化为α，2β化为β）；
（3）函数名称为正弦、余弦（可以利用平方关系进行名称的统一）；
（4）共有3项（需要减少），由于侧重角度不同，出发点不同，本题化简方法不止一种。
解法一：
解法二：（从“名”入手，异名化同名）
解法三：（从“幂”入手，利用降幂公式先降次）
解法四：（从“形”入手，利用配方法，先对二次项配方）
［注］在对三角式作变形时，以上四种方法，提供了四种变形的角度，这也是研究其他三角问题时经常要用的变形手法。
例9. 
形ABCD，（如图），求该矩形的最大面积。
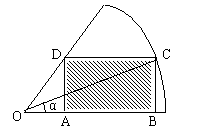
分析：欲求矩形的最大面积，按照函数的思想就是求面积函数的最大值，因此需要先依照题意，建立面积函数，选哪个量作自变量呢？经尝试发现：选取∠COB=α为面积函数的自变量最优，于是可建立一个以角α为自变量的三角函数来表示矩形面积，进而研究该函数的最值即可。
解：
【模拟试题】
一. 选择题
1. 函数
的图象的一条对称轴方程是（ ）
A. 
B.
C. 
D.
2. 下列函数中，以
为周期的函数是（ ）
A. 
B. 
C. 
D. 
3. 函数
A. 增函数 B. 减函数
C. 偶函数 D. 奇函数
4. 函数
的最小值为（ ）
A. 
B.
C. 0 D. 1
5. 若点P
在第一象限，则在［０，2
］内
的取值范围是（ ）
A. 
B. 
C. 
D. 
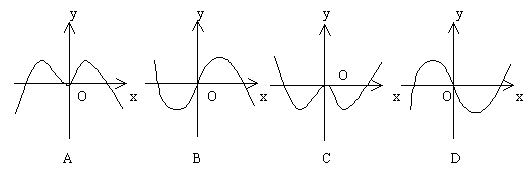
6. 函数
的部分图象是（ ）
7. 若
x的取值范围是（ ）
A. 
B. 
C. 
D. 
8. 已知
是第三象限的角，若
等于（ ）
A. 
B.
C. 
D.
9. 已知是第三象限的角，且
=（ ）
A. B.
C.
D.
10. 当
A. 最大值为1，最小值为-1
B. 最大值为1，最小值为
C. 最大值为2，最小值为
D. 最大值为2，最小值为
二. 填空题
11. 函数
的最小正周期为__________
12. 已知
__________
13. 函数
的最大值为__________。
14. 求值：
__________
15. 
角A、B、C的对边分别为a、b、c，若
，则△ABC的形状是___________。
16. 求值：
=_______________
二. 解答题：
17. 已知
的值
18. 在
分别是角A、B、C的对边，设
，求sinB的值。
19. 已知函数
，
（I）当y取最大值时，求自变量x的集合；
（II）该函数的图象可由y=sinx，
的图象经过怎样的平移和伸缩变换得到？
【试题答案】
一. 选择题
1. 选（A）
提示：由
的图象可知，若其对称轴方程
，则y取最值，故只需求出使y取最值时的
即可得到对称轴方程。显然当
时，y取最值，
，
。
2. 选（D）
提示：把A、B、C、D选择支中的函数解析式变形为
后，易由
的只有（D）
3. 选（C）
提示：
4. 选（A）
提示：
y有最小值
5. 选（B）
提示：
6. 选（D）
提示：显然
7. 选（D）
提示：
8. 选（A）
提示：
9. 选（C）
提示：利用半角公式
10. 选（D）
提示：
，而
二. 填空题
11. 最小正周期
12. 
提示：
两边同时平方，有
求出
13. 最大值为
提示：
14. 
提示：利用公式
可把
15. 
是等腰三角形或直角三角形
提示：利用正弦定理，有
从而
16. 原式=
提示：
原式
三. 解答题
17. 解：由
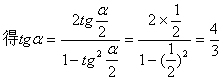
若是第一象限的角，则
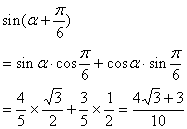
若是第三象限的角，则
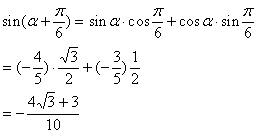
18. 解：由正弦定理及
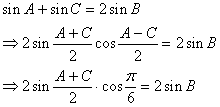
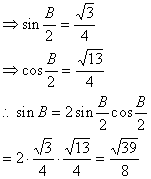
19. 解：（I）
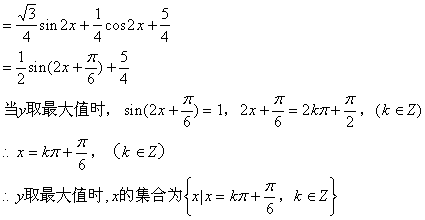
（II）把
图象向左平移
个单位，得
的图象，再把该图象上每点的横坐标缩短为原来的，得
的图象；最后把该图象上所有的点都向上平移
个单位，得到
的图象。
| 年级 | 高三 | 学科 | 数学 | 版本 | 人教版 | 期数 | 3428 | |||||
| 内容标题 | 三角函数与三角变形 | |||||||||||
| 分类索引号 | G.623.3 | 分类索引描述 | 学习资料 | |||||||||
| 主题词 | 三角函数与三角变形 | 栏目名称 | 同步课堂 | |||||||||
| 编稿老师 | 胡顺才 | 审稿老师 | 李欣生 | |||||||||
| 录入 | 韩素果 | 一校 | 康纪云 | 二校 | 刘连静 | 审核 | ||||||