高三数学综合练习（0301）
一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是最符合题目要求的）
1.设全集Ｉ＝｛1，3，5，7，9｝，集合A＝｛1，｜a－5｜，9｝，
＝｛5，7｝，则A的值是
A.2 B.８ C.－2或8 D.2或8
2.下列函数的图象中，经过平移或翻折后不能与函数
的图象重合的函数是
A.
B.
C.
D.
3.等边△ABC的顶点A、B、C按顺时针方向排列，若复平面内，A、B两点对应的复数分别为－1＋2
ｉ和1，则C点对应的复数为
A.－2 B.－2－ｉ
C.-2-I
D.-3
4.已知直线m、n、l，平面α、β，以下命题中，正确命题的个数是
(1)若m∥α，n∥α，则m∥n
（2）若α⊥β，m⊥l，l
β则m⊥β
(3)若m、n为异面直线，m∥α，则n与α相交
(4)若m⊥n，m⊥α，n
α则n∥α
A.0 B.1 C.2 D.3
5.甲、乙、丙三个单位分别需要招聘工作人员2名、1名、1名，现从10名应聘人员中招聘4人到甲、乙、丙三个单位，那么不同的招聘方法共有
A.1260种 B.2025种 C.2520种 D.5040种
6.设ｗ∈R+，如果y＝2sinwx在［－
，
］上单调递增，那么ｗ的取值范围是
A.
B.
C.
D.
7.直线(x＋1)a＋（y＋1）b＝0与圆x2＋y2＝2的位置关系是
A.相交 B.相切 C.相离 D.相交或相切
8.设θ是三角形的一个内角，且sinθ＋cosθ＝
，则方程x2sinθ－y2cosθ＝1表示
A.焦点在x轴上的椭圆 B.焦点在y轴上的椭圆
C.焦点在x轴上的双曲线 D.焦点在y轴上的双曲线
9.等比数列｛an｝的公比为q，则“a1＞0，且q＞1”是“对于任意自然数n，都有an+1＞an”的
A.充分非必要条件 B.必要非充分
C.充要条件 D.既非充分又非必要条件
10.已知f（x）是奇函数，定义域为｛x｜x∈R，x≠0｝，又f（x）在区间(0，＋∞)上是增函数，且f（－1）＝0，则满足f（x）＞0的x的取值范围是
A.（1，＋∞） B.（0，1）
C.（－1，0）∪（1，＋∞） D.（－∞，－1）∪（1，＋∞）
11.数列｛an｝中，a1＝1，Sn是前n项和，当n≥2时，an＝3Sn，则
的值是
A.－
B.－2
C.1
D.－
12.对于抛物线C：y2＝4x，我们称满足y02＜4x0的点M(x0，y0)在抛物线内部，若点M(x0，y0)在抛物线内部，则直线l：y0y＝2（x＋x0）与C
A.恰有一个公共点 B.恰有两个公共点
C.可能一个公共点，也可能两个 D.没有公共点
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
13.若
的展开式中第三项系数为36，则自然数n的值是 .
14.若集合{(x，y)x+y-2=0且x-2y+4=0}{(x，y)y=3x+b}，则b= .
15.已知函数f（x）＝｜x2－2ax＋b｜(x∈R)，给出下列命题：①f（x）必是偶函数；②当f（0）＝f（2）时f（x）的图象必关于直线x＝1对称；③若a2－b≤0，则f（x）在区间
上是增函数；④f（x）有最大值a2－b，其中正确命题序号是
.
16． {an}是由实数构成的无穷等比数列，
关于数列
，给
出下列命题：
①数列中任意一项均不为0；
②数列中必有一项为0；
③数列中或者任意一项均不为0，或者有无穷多项为0；
④数列中一定不可能出现Sn=Sn+2;
⑤数列中一定不可能出现Sn=Sn+3;
则其中正确的命题是 .（把正确命题的序号都填上）
数学答卷（0301）
高三 班 坐号 姓名 得分
一、
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、
13. 。 14. 。
15. 。 16. 。
三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）
17.(本小题满分12分)
设复数
，
满足
，
，且
，求
．
18.(本小题满分12分)
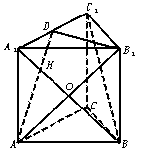
如图正三棱柱ABC－A1B1C1的底面边长为2，侧棱长为，A1C1的中点为D.
(Ⅰ)求证BC1∥平面AB1D；
(Ⅱ)求二面角A1－B1D－A的大小；
(Ⅲ)求点B到平面AB1D的距离.
19.(本小题满分12分)
已知f（x）＝2x－1的反函数为
（x），g（x）＝log4（3x＋1）.
(Ⅰ)若f-1（x）≤g（x），求x的取值范围D；
(Ⅱ)设函数H（x）＝g（x）－
（x），当x∈D时，求函数Ｈ（x）的值域.
20.(本小题满分12分)
某种商品进价80元，零售价每个100元，为了促进销售可以采取买一个这种商品，赠送一个小礼品的办法.实践表明：礼品价值为1元时，销售量增加10%，且在一定范围内，礼品价值为n＋1元时，比礼品价值为n元(n∈N)时的销售量增加10%.
(Ⅰ)写出礼品价值n元时，利润yn(元)与n的函数关系式；
(Ⅱ)请你设计礼品价值，以使商店获得最大利润.
21.(本小题满分12分)
以y轴为右准线的双曲线C经过点M(1，2)，它的右焦点F在曲线
(x－1)2＋（y－2）2＝4（x＞0)上.
(Ⅰ)当MＦ∥x轴时，求双曲线C方程；
(Ⅱ)求直线MＦ与双曲线C右支的另一个交点N的轨迹方程.
22.(本小题满分14分)
对于函数f（x），若存在x0∈R,使f（x0）＝x0成立，则称x0为f（x）的不动点.如果函数f（x）＝ax2＋bx＋1（a＞0）有两个相异的不动点x1，x2.
(Ⅰ)若x1＜1＜x2<2，且ｆ（x）的图象关于直线x＝m对称,求证：＜m＜1；
(Ⅱ)若｜x1｜＜2且｜x1－x2｜＝2，求b的取值范围.
综合练习（0301）参考答案
一、1.D 2.C 3.D 4.B 5.C 6.A 7.D 8.B 9.A 10.C 11.A 12.D
二、 13.9 14. 2 15.③ 16.1、4
三、17.解：设
由已知，得
|
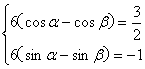
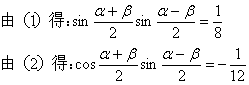
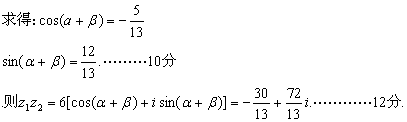
18.(Ⅰ)证明：连结A1B，设A1B与AB1相交于O，则O为A1B的中点，连结DO，因D为A1C1中点，所以DO为△A1BC1的中位线，∴DO∥BC1又DO平面AB1D，BC1平面AB1D ∴BC1∥平面AB1D 
∥平面AB1D
4分
(Ⅱ)解：由题意知，B1D是正△A1B1C1的中线，
∴A1C1⊥B1D在正三棱柱ABC－A1B1C1中，AA1⊥平面A1B1C1 ∴AD⊥B1D，∴∠ADA1是二面角A1－B1D－A的平面角，在Rt△ADA1中，tgADA1＝
∴∠ADA1＝60°即二面角A1－B1D－A等于60° 8分
(Ⅲ)解：因为O为A1B的中点，所以点B到平面AB1D的距离等于点A1到平面AB1D的距离.由(Ⅱ)知B1D⊥平面A1ACC1 ∴平面AB1D⊥平面A1ACC1且平面AB1D∩平面A1ACC1＝AD，过点A1作A1H⊥AD，垂足为H，则A1H⊥平面A1BD，所以线段A1H的长度就是点A1到平面AB1D的距离
在Rt△A1AD中，
∴点B到平面AB1D距离为
12分
19.解：(Ⅰ)∵
∴
(x＞-1) 2分
由
≤g（x） ∴
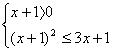14分
解得0≤x≤1 ∴D＝［0，1］ 6分
(Ⅱ)H（x）＝g（x）－
9分
∵0≤x≤1 ∴1≤3－
≤2
∴0≤H（x）≤ ∴H（x）的值域为［0，］ 12分
20.解：（Ⅰ）设未赠礼品时销售量为ｍ件，则当礼品ｎ元时，销售量为ｍ（1＋10％）n，利润yn＝（100－80－ｎ）·ｍ·（1＋10％）n＝（20－ｎ）ｍ×1.1n（0＜ｎ＜20，ｎ∈N)4分
(Ⅱ)设礼品赠送ｎ元时，利润最大
则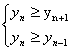
8分
∴9≤ｎ≤10 10分
∴礼品价值为9元或10元时，商店获利最大12分
21.解：(Ⅰ)可知M为圆心，
，F(3，2)，M为右顶点
2分
设双曲线方程为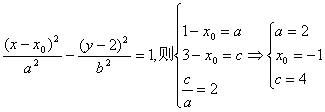
即双曲线方程为
6分
(Ⅱ)设N（x，y）（x＞0），则｜
∴9（x＋
）2－3（y－2）2＝16（x＞0）
12分
22.(Ⅰ)证明：g（x）＝f（x）－x＝ax2＋（b－1）x＋1且a＞0 ∵x1＜1＜x2＜2
∴（x1－1）（x2－1）＜0即x1x2＜（x1＋x2）－1 2分
于是
＞
［（x1+x2）-1］=
4分
又∵x1＜1＜x2＜2 ∴x1x2＞x1于是有ｍ＝（x1＋x2）－x1x2＜（x1＋x2）－x1＝x2＜1 ∴＜m＜1
6分
(Ⅱ)解：由方程
＞0，∴x1x2同号
（ⅰ）若0＜x1＜2则x2－x1＝2
∴x2＝x1＋2＞2 ∴g（2）＜0
即4a＋2b－1＜0 ①
又(x2－x1)2＝
8分
∴
，（∵a＞0）代入①式得
＜3－2b，解之得：b＜
10分
(ⅱ)若－2＜x1＜0，则x2＝－2＋x1＜－2 ∴g（－2）＜0，即4a－2b＋3＜0 ②
又代入②得＜2b－1解之得b＞
综上可知b的取值范围为
14分