高三月考数学试卷4

高三月考数学试卷4

　　本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分，考试时间120分钟。

第Ⅰ卷（选择题　共45分）

一、选择题：本题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一

项是符合题目要求的.

1．的最小正周期是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．

2．直线在y轴上的截距是－1，且它的倾斜角是直线的倾斜

　 角的2倍，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　D．

3．已知直线平面，，直线平面，对于以下四个命题： ①；

　 ②；③；④.其中真命题是　　　（　　）

　　　 A．①②　　　　　　　　　 B．③④　　　　　　　　　 C．①③　　　　　　　　　 D．②④

4．从4种不同的小麦品种中选出3种种在3块土质不同的试验田进行试验，不同的实验方

　 案种数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　 B．　　　　　　　　　　 C．3⁴　　　　　　　　　　　 D．4³

5．已知　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　 D．－

6．的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．充要条件　　　　　　　　　　　　　　　　　　　　　 B．充分不必要条件

　　　 C．必要不充分条件　　　　　　　　　　　　　　　　 D．既不充分又不必要条件

7．抛物线的焦点坐标是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　B．　　　　　　　C．　　　　　　 D．

8．若函数的值域是，则它的定义域是　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　B．（0，2）　　　　　　　C．（0，4）　　　　　　　D．（2，4）

9．将抛物线的图象按向量平移，使其顶点与坐标原点重合，则=（　　）

　　　 A．（2，3）　　　　　　　B．（－2，－3）　　　 C．（－2，3）　　　　　D．（2，－3）

10．在直角三角形中两锐角为A和B，则cosAcosB的取值范围是　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　B．（0，1）　　　　　　　C．　　　　　　　　 D．

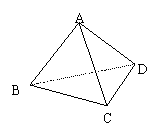11．四面体A—BCD中，，其余棱长均为1，则二面

角A—BC—D的大小是　　　　　　　　　　  （　　）

A． 　　　　　　　　　　B．

C．　　　　 D．

12．某工厂1997至2000年产量和为100吨，1999年至2002年产量和为121吨，则该工厂

从1997年至2002年产量的年平均增长率是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．10%　　　　　　　　　 B．11%　　　　　　　　　　C．14%　　　　　　　　　 D．21%

二、填空题：本大题共4个小题，每小题4分，共16分，把答案填在题中横线上.

13．的展开式的第4项是　　　　　　　 .

14．长方体三个面的对角线长分别是a、b、c，则它的对角线长是　　 　　　　 .

15．若双曲线的一条准线恰好是圆的一条切线，则实数k的

值是　　　　　　  .

16．读下列命题，请把正确命题的序号都填在横线上　　　　　　  .

①若函数对定义域中的x总有是偶函数；

②函数的图象关于直线x=2对称；

③函数的图象关于直线对称；

④函数的反函数的图象关于点（－2，－1）中心对称.

三、解答题：本大题6个小题，共74分，解答题应写出文字说明、证明过程和演算步骤.

17．（本小题满分12分）

设集合，若，求实数a的取值范围.

18．（本小题满分12分）

已知是等差数列，其前n项和为S_n，已知a₂=8，S₁₀=185，

　 （1）求数列的通项公式；

　 （2）设，证明是等比数列，并求其前n项和T_n.

19．（本小题满分12分）

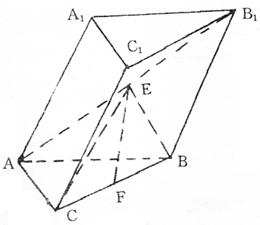
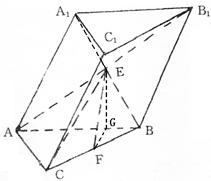
如图，斜三棱柱ABC—A₁B₁C₁的底面是直角三角形，AC⊥CB，∠ABC=45°，侧面

A₁ABB₁是边长为a的菱形，且垂直于底面ABC，∠A₁AB=60°，E、F分别是AB₁、

BC的中点.

　 （1）求证EF//平面A₁ACC₁；

　 （2）求EF与侧面A₁ABB₁所成的角；

　 （3）求三棱锥A—BCE的体积.

20．（本小题满分12分）

一个电路中有三个电子元件，它们接通的概率都是m（0＜m＜1如图，有如下三

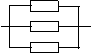种联接方法：

①　　　　　　　　　　　　　  ②　　　　　　　　 ③

　 （1）分别求出这三种电路各自接通的概率；

　 （2）试分析这三种电路哪种性能最优，并证明你的结论.

21．（本小题满分12分）

　　已知直线经过椭圆的右焦点F₂，且与

椭圆C交于A、B两点，若以弦AB为直径的圆经过椭圆的左焦点F₁，试求椭圆C的方

程.

22．（本小题满分14分）

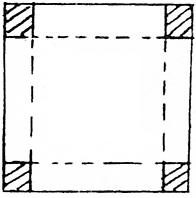
　　把边长为4的正方形铁片的四个角各截去一个边长为x的小正方形，再将四边沿虚

线向上折起，做成一个无盖的方底铁盒.

　 （1）把铁盒容积V表示为x的函数V（x），并指出其定义域；

　 （2）确定V（x）的单调区间；

　 （3）若要求铁盒的高度x与底面正方形边长的比值不超过常数a，x取何值时，铁盒容积

有最大值？

高三月考数学试卷参考答案

一、BCCBD　 CABDA　 DA

二、13． 960x³　 14．　 15． 8　　16．③④

三、17．…………2分　　……5分

……8分　……10分

实数a的取值范围是：…………12分

18．（1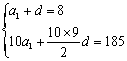）………3分　　解得……5分　……6分

　 （2）……7分  是公比为8的等比数列……10分

　 ……12分

19．（1）∵A₁ABB₁是菱形，E是AB₁中点， ∴E是A₁B中点，

连A₁C　∵F是BC中点， ∴EF∥A₁C…………12分

∵A₁C平面A₁ACC₁，EF平面A₁ACC₁， ∴EF//平

面A₁ACC₁……………4分

（2）作FG⊥AB交AB于G，连EG　∵侧面A₁ABB₁⊥平

面ABC且交线是AB　∴FG⊥平面A₁ABB₁，∴∠FEG是

EF与平面A₁ABB₁所成的角…………6分

由AB=a，AC⊥BC，∠ABC=45°，得　由AA₁=AB=a，∠A₁AB=60°，

得　…………8分

（3）V_A—BCE=V_E—ABC　由②EG⊥AB，平面A₁ABB₁⊥平面ABC，∴EG⊥平面ABC…………10分

………………12分

20．（1）三种电路各自接通分别记为事件A₁、A₂、A₃，则P（A₁）=m³…………3分

P（A₂）=1－（1－m）³=3m－3m²+m³………6分　 P（A₃）=2（1－m）m²+m³=2m²－m³……9分

（2）P（A₂）－P（A₁）=3m－3m²=3m（1－m）　 ∵0＜m＜1　 ∴P（A₂）＞P（A₁）………10分

P（A₂）－P（A₃）=2m³－5m²+3m=m（2m－3）（m－1）＞0　　∴P（A₂）＞P（A₃）…………11分

三个电子元件并联接通的概率最大，故性能最优………………12分

21．设椭圆焦距为2c，则………1分　 ，代入y=x+k　得k=－1……2分

将y=x－1代入椭圆方程整理得：…………4分

∵A、B点在直线l上，设　∵AF₁⊥BF₁　又F₁（－1，0）

…………7分　由韦达定理，

解得……10分　

为所求方程.…………12分

22．（1） ……2分　由得函数定义域是…………4分

（2）　　　

令（舍）……6分　当，

当　故V（x）在区间上是增函数，在区间上是减函数……8分

（3）由题意，　解得V（x）的定义域是…………10分

其中　　由（2）结论，当上

是增函数时，V（x）有最大值…………12分　　当在

上增，在上减　 有最大值.…………14分