| 数学高考复习综合能力题选讲(二) 本刊试题研究小组 “立足基础,突出能力考查;从学科整体知识结构和思想体系上考虑问题,加强试题的综合性和应用性;创设新颖的情景和设问方式”构成了高考命题(数学科)的主旋律.这使得高考试卷中综合能力题的分量越来越重,如1999年试卷中几何类的综合能力题就包括客观题的第(6)、(10)、(13)、(18)题,主观题的第(24)题等.通过综合知识来完成“逻辑思维能力、运算能力、空间想象能力、分析问题和解决问题的能力”的考查入情入理,而解答综合能力 题离不开数学的基本思想和基本方法的指导和运用.这就要求我们在平时的教学中注意和重视数学基本思想和方法的渗透和掌握,加强能力培养,教会学生善于抓住问题的实质,对所给问题提供的信息能进行分解、组合和加工,以便寻找解决问题的方法.另外,“增加思考量,控制计算量”值得我们在几何复习中深思.
例1某人买了一罐容积为V升、高为a米的直三棱柱型罐装进口液体车油,由于不小心摔落地上,结果有两处破损并发生渗漏,它们的位置分别在两条棱上且距下底面高度分别为b、c的地方(单位:米).为了减少罐内液体油的损失,该人采用破口朝上,倾斜罐口的方式拿回家.试问罐内液体油最理想的估计能剩多少.
讲解:首先据题目叙述画出示意图(图1).直三棱柱为ABC-A′B′C′,破损处为D、E,并且AD=b,EC=c,BB′=a. 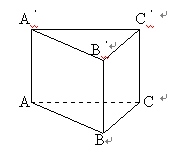
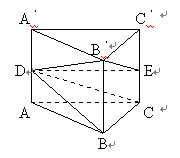
图1 图2 其次,是理解“最理想的估计能剩多少”这句话,并将其翻译为数学语言--“罐内所剩液油的最大值为多少?”
再次,是想象什么时候才能达到该最大值.显然,过D、E两点的平面同时应过B′,才可达到要求.故问题转化为求几何体ABCDB′E的体积.
最后,为求该不规则几何体的体积还应对图形进行处理,办法不惟一,仅给出一种如下:
因为VABC-DB′E=VD-BCEB′+VD-ABC,而VD-ABC=bV/3a,故只需求VD-BCEB′,参见图2.
由VD-BCEB′VA′-BCC′B′=(a+c)/2a及VA′-BCC′B′=(2/3)V,可求得VD-BCEB′=(a+c)V/3a.
于是,最理想的估计是剩下(a+b+c)V/3a升.
说明:该题的背景为学生所熟悉,考查了学生阅读理解、空间想象及处理图形的能力.
例2如图3所示,在矩形ABCD中,已知AB=1,BC=a,PA⊥平面ABCD,且PA=1. 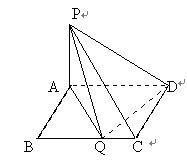
图3 (1)在BC边上是否存在点Q,使得PQ⊥QD,说明理由;
(2)若BC边上有且仅有一个点Q,使PQ⊥QD,求AD与平面PDQ所成角的正弦值;
(3)在(2)的条件下,能求出平面PQD与平面PAB所成的角的大小吗?
讲解:对于(1)假设边BC上存在Q点,使得PQ⊥QD,则连结AQ,必有∠ AQD=90°,反之亦然,故问题转化为:在边BC上是否存在点Q,使得∠AQD=90°.
由平面几何知识,问题又可转化为:以AD为直径作圆,是否与BC边有公共点?
易知,当AB≤(1/2)AD时,即a≥2时,BC边上存在点Q,使得∠AQD=90°,从而PQ⊥QD;当AB>(1/2)AD时,即a<2时,不存在点Q,使得PQ⊥QD.
若通过引入线段参数,构造一元二次方程,利用判别式也可得到解答,留给读者完成.( 提示:设CD=x,由勾股定理建立方程.)
对于(2),当BC边上有且仅有一个点Q,使得PQ⊥QD,可知BC=2,点Q为BC的中点,过A在平面PAQ上作AF⊥PQ,垂足为F,连结FD,则∠FDA是直线AD与平面PQD所成的角.可求得sin∠FDA=AF/AD=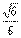 . .
对于(3),留给读者思考.
说明:该题考查了学生利用所学知识探索求解问题的能力.体现出转化的思想.
例3若方程x+y-6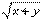 +3k=0仅表示一条直线,则实数k的取值范围是____. +3k=0仅表示一条直线,则实数k的取值范围是____.
讲解:一个二元一次方程与一条直线对应,而所给方程为无理方程,必须对其进行求解转化为x+y=m的形式方可.
显然应有x+y≥0,故所给方程即
(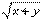 )2-6 )2-6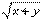 +3k=0.(*) +3k=0.(*)
视x+y为一个整体,则其有解必先满足
Δ=36-12k≥0,得k≤3.
在k≤3的前提条件下,若方程(*)有零根,必有k=0,此时,可由(*)解得
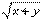 =0, =0,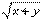 =6,即 x+y=0,x+y=36. =6,即 x+y=0,x+y=36.
得到了两条直线的方程,表示两条直线,与题设要求不符,故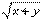 不能为零.从而关于 不能为零.从而关于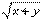 的二次方程(* )的根的情况包括三种可能:两正,两负,一正一负.但两负的情况与题设要求不相符.故有 的二次方程(* )的根的情况包括三种可能:两正,两负,一正一负.但两负的情况与题设要求不相符.故有
若从方程(* )中解出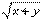 等于两个正数,除非其相等,才能满足题设.由Δ=0得k=3,且 等于两个正数,除非其相等,才能满足题设.由Δ=0得k=3,且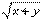 =3,即x+y=9,满足题设; =3,即x+y=9,满足题设;
若从方程(* )中解出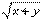 等于一个正数及一个负数,则必有负数被舍,仅得 等于一个正数及一个负数,则必有负数被舍,仅得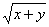 等于正数,也满足题设.由两根之积小于零得k<0. 等于正数,也满足题设.由两根之积小于零得k<0.
综合知k<0或k=3为所求.
说明:该题以曲线和方程的概念为切入点,考查了根与系数的关系,分类讨论的思想,转化的思想,以及考生综合运用所学知识分析问题、解决问题的能力.
例4已知抛物线的方程为y=-(1/2)x2+m,点A、B及P(2,4)均在抛物线上,且直线PA、PB的倾斜角互补.
(1)求证:直线AB的斜率为定值;
(2)当直线AB在y轴上的截距为正时,求△PAB面积的最大值. 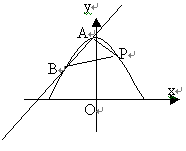
图4 讲解:由点P在抛物线上,可求得抛物线的方程为y=-(x2/2)+6,从而可画出该抛物线(如图4所示).由图4知PA的斜率k存在,且k≠0,则PA的方程为y-4=k(x-2).由直线PA、PB的倾斜角互补知,PB的方程为y-4=-k(x-2).
(1)设A、B两点的坐标为(x1,y1),(x2,y2),则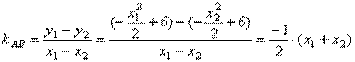 . .
为得x1+x2,我们将PA、PB的方程分别代入抛物线方程并整理得
x2+2kx-4k-4=0,x2-2kx+4k-4=0.
由韦达定理有x1+2=-2k,x2+2=2k,
故kAB=-1/2×(-4)=2(定值).
(2)设AB的方程为y=2x+b(b>0),将其代入抛物线方程并整理得
x2+4x+2b-12=0.
由Δ>0及b>0,得0<b<8.
点P到AB的距离为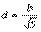 ,又由弦长公式可得 ,又由弦长公式可得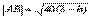 ,故 ,故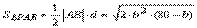 . .
欲求S△PAB的最大值,须借助三元均值不等式,还得凑系数,以达到“一正二定三相等”的要求.结果为当b=16/3时,S△PAB最大,最大值为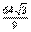 . .
说明:本题巧妙地将直线与抛物线融合在一起,既涉及到定值,又“牵连”到最值问题,既要借助韦达定理、弦长公式,又需用三元均值不等式,“动中求静”、“变中求定”,考查了解析几何的基本思想和方法,考查了综合运用知识的能力.值得提醒的是:由Δ>0及b>0得0<b<8这一步,常常被考生忽视.而在有关直线与圆锥曲线的试题中又常常被设计为“存在性”问题.
例5某校初一年级为配合素质教育,利用一间教室作为学生绘画成果展室.为节约经费,他们利用课桌作为展台,将装画的镜框放置在桌上,斜靠墙壁展出.已知镜框对桌面的倾角为θ(90°≤θ<180°),镜框中,画的上、下边缘与镜框下缘分别相距a米、b米(a>b).问:学生距镜框下缘多远看画的效果最佳?
讲解:从理论上来讲,视角最大时看画的效果最佳(不考虑其他因素).我们需做这样的设想才能把其抽象为一个数学问题,眼睛看成一个点,眼睛的高度与镜框下缘所处的高度相同,视线向正前方,画可以看成由无数条与镜框下缘垂直的线条连成的.故利用二面角的所在平面建立坐标系xOy,参见图5,将问题转化为:“已知∠xOA=α,OA=a,OB=b,在Ox轴的正方向上求一点C,使∠ACB取最大值.”
设C点的坐标为(x,0)(x>0),则A、B两点的坐标分别为(acosθ,asinθ)、(bcosθ,bsinθ).于是直线AC、BC的斜率可求. 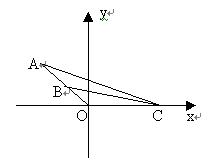
图5 由到角公式,得
tg∠ACB=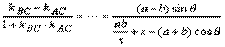 . .
因∠ACB是锐角,所以有
tg∠ACB≤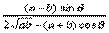 , ,
当且仅当ab/x=x,即x=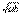 时,等号成立,此时∠ACB取最大值,对应的点为C( 时,等号成立,此时∠ACB取最大值,对应的点为C(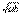 ,0). ,0).
因此,学生距镜框下缘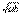 米时视角最大,此时看画的效果最佳. 米时视角最大,此时看画的效果最佳.
说明:该题是实际问题,涉及到空间想象,难在将其抽象为解析几何中的问题,对分析和解决问题的能力要求极高!
以下题目供复习时参考:
1.正四面体与正四棱锥的侧面全等,它们放成一侧面重合后得到一个多面体,这个多面体的面数是____.
2.如图6,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个命题:①水的部分始终呈棱柱形;②水面四边形EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜如图7所示时,BF·BE是定值.其中所有正确命题的序号是. 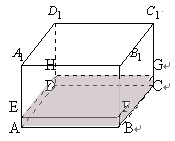
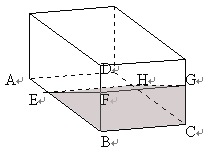
图6 图7 3.过椭圆x2/9+y2/5=1的左焦点作一条长为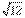 的弦AB,将椭圆绕其左准线在空中旋转120°,则弦AB扫过的面积为_____. 的弦AB,将椭圆绕其左准线在空中旋转120°,则弦AB扫过的面积为_____.
4.三棱锥S-ABC的底面是边长为a的正三角形,A在侧面SBC上的射影H是△SBC的垂心,且二面角H-AB-C的大小为30°.
(1)证明三棱锥S-ABC是正三棱锥;(2)求侧棱与底面所成的角;(3)求侧面与底面所成的二面角;(4)求三棱锥S-ABC的体积.
5.以椭圆x2/a2+y2=1(a>1)的短轴端点B(0,1)为直角顶点作椭圆的内接等腰△ABC,问这样的三角形能作出几个?
6.已知抛物线C1:y2=x+1,C2:(x+1/4)2=1/2(y-19/8),直线l:y=kx+b.试问是否存在自然数k和b,使l与C1、C2均无公共点.
7.直线l:ax-y-1=0与双曲线C:x2-2y2=1相交于P、Q两点.
(1)当实数a为何值时,PQ=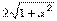 ; ;
(2)是否存在实数a,使得以PQ为直径的圆经过坐标原点.若存在,求出a的值;若不存在,说明理由.
8.舰A在舰B的正东方向6千米处,舰C在舰B的北偏西30°且距舰B4千米处,三艘舰围捕某海洋动物.在某时刻舰A收到了该动物发出的某种信号,B、C两舰在4秒后同时收到了这种信号.由舰A向该动物发射麻醉炮弹.设舰与动物均为静止的,动物信号的传播速度是1千米/秒,炮弹运行的初速度是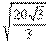 g千米/秒,其中g是重力加速度.若不计空气阻力与舰高,求舰A发射炮弹的方位角和仰角. g千米/秒,其中g是重力加速度.若不计空气阻力与舰高,求舰A发射炮弹的方位角和仰角.
9.已知E是矩形ABCD的边CD的中点,且CD=2,BC=1.现沿AE将△DAE折起至△D′AE,使得D′到B、C两点的距离相等.
(1)求证:面D′AE⊥面ABCE;
(2)求二面角D′-BC-A的正切值;
(3)求A点到面D′BC的距离.
10.如图8所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正向成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为定值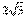 . . 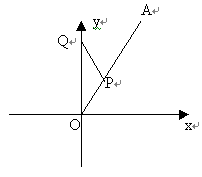
图8 (1)求线段PQ的中点M的轨迹C的方程;
(2)R1、R2是曲线C上的动点,R1、R2到y轴距离之和为1,设u为R1、R2到x轴距离之积,是否存在最大的常数m,使u≥m恒成立?如果存在,求出这个m的值;如果不存在,请说明理由.
参考答案
1.5. 2.①、③、④. 3.6π. 4.(1)略;(2)60°;(3)arctg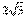 ;(4) ;(4)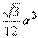 . 5.当1<a≤ . 5.当1<a≤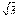 时,满足题设条件的等腰直角三角形只有一个;当a> 时,满足题设条件的等腰直角三角形只有一个;当a>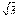 时,满足题设条件的直角等腰三角形有三个. 6.存在,k=1,b=2时满足. 7.(1)a= ±1;(2)假设存在,得出a2=-2,与a为实数矛盾,故不存在实数a,使得以PQ为直径的圆经过原点. 8.取AB所在直线为x轴,线段AB的垂直平分线为y轴建立直角坐标系,则A(3,0),B(-3,0),C(-5,2 时,满足题设条件的直角等腰三角形有三个. 6.存在,k=1,b=2时满足. 7.(1)a= ±1;(2)假设存在,得出a2=-2,与a为实数矛盾,故不存在实数a,使得以PQ为直径的圆经过原点. 8.取AB所在直线为x轴,线段AB的垂直平分线为y轴建立直角坐标系,则A(3,0),B(-3,0),C(-5,2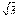 ),据题知动物所处位置在线段BC的中垂线 ),据题知动物所处位置在线段BC的中垂线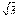 x-3y+7 x-3y+7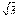 =0……①上,又由|PB|-|PA|=4知动物所处的位置点P又在双曲线x2/4-y2/5=1……②的右支上,联立①、②解得点P的坐标为(8,5 =0……①上,又由|PB|-|PA|=4知动物所处的位置点P又在双曲线x2/4-y2/5=1……②的右支上,联立①、②解得点P的坐标为(8,5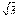 ),于是|PA|=10,∵ kPA= ),于是|PA|=10,∵ kPA=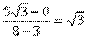 ,∴ ∠xAP=60°.∴ 舰A发射炮弹的方位角为北偏东30°. ,∴ ∠xAP=60°.∴ 舰A发射炮弹的方位角为北偏东30°.
设发射炮弹的仰角为θ,则据运动学原理有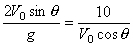 ,即 ,即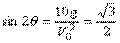 ,∴ 仰角θ=30°. 9.(1)略;(2) ,∴ 仰角θ=30°. 9.(1)略;(2)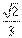 ;(3) ;(3)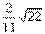 . 10.(1) . 10.(1)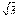 x2-xy+ x2-xy+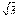 =0(x>0,y>0);(2)mmax=75/4=umin. =0(x>0,y>0);(2)mmax=75/4=umin. | 



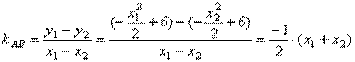 .
.


