数学高考模拟考试试题
第I卷（共60分）
参考公式：如果事件A、B互斥，那么
如果事件A、B相互独立，那么
一．选择题：本大题共12小题，每题5分，共60分，在每小题给出的四个选项中，选择一个符合题目要求的选项．
（1）如果
，
，那么（ ）
（A）
（B） （C）
（D）
（2）已知
是偶函数，当
时，
；当
时，
（ ）
（A）
（B）
（C）
（D）
（3）a、b、c成等比数列，关于x的方程
（ ）
（A）一定有两个不相等的实数根 （B）一定有两个相等的实数根
（C）一定没有实数根 （D）以上三种情况均可能出现
（4）要得到
的图象，只需将
的图象（ ）
（A）向左平移
个单位 （B）向右平移个单位
（C）向左平移
个单位 （D）向右平移个单位
（5）已知A(2，1)，B(3，5)把
按向量（3，2）平移后得到一个新向量
．那么下列各向量中能与垂直的是（ ）
（A）（– 4，1） （B）（
，
） （C）（– 4，6） （D）（0，– 2）
（6）设
、
是二次方程
的两实根，则
有（ ）
（A）最小值为
（B）最小值为8
（C）最小值为最大值为8 （D）无最值
（7）不论m为何实数，直线
恒过一定点．此点是（ ）
（A）（2，3） （B）（– 2，3） （C）（0，
） （D）（– 2，0）
（8）已知直线经过点（– 1，2）且方向向量为（2，3），则直线方程为（ ）
（A）
（B）
（C）
（D）
（9）抛物线
的准线方程为
，则a的值为（ ）
（A）
（B）
（C）8 （D）– 8
（10）对于空间任意一点O和不共线的三点A、B、C，且有
（x、y、z
R），则
是四点P、A、B、C共面的（ ）
（A）必要条件 （B）充分条件 （C）充要条件 （D）既不充分又不必要条件
（11）在
的展开式中，各项的二项式系数的和是（ ）
（A）1或 – 1 （B）1 （C）
（D）– 1
（12）一个学生通过某种英语测试的概率是，他连续测试n次，要保证他至少有一次通过的概率大于0.9，那么n的最小值为（ ）
（A）3 （B）4 （C）5 （D）6
二．填空题：本大题共4小题，每小题4分，共16分．答案须填在题中横线上．
（13）将一组数据
，
，…，
改变为
，
，…，
，则前后方差的关系为
．
（14）
在点P( – 1，1)处的切线方程为
．
（15）一动圆与圆
外切，同时与圆
内切，则动圆圆心的轨迹是
．
（16）5张票中有两张奖票（后抽的人不知道先抽的人抽出的结果），则第4人抽到奖票的概率为 ．
高考模拟考试试题
数 学
第I卷（共60分）
一．选择题：本大题共12小题，每题5分，共60分．
1~5． 5~10． 11~12．
第II卷（共90分）
二．填空题：本大题共4小题，每小题4分，共16分．
13． 14．
15． 16．
三．解答题：本大题共6小题，共74分．解答写出文字说明，证明过程或演算步骤．
（17）（本小题满分12分）
已知函数
（其中
，
）的图象在y轴右侧的第一个最高点（函数取最大值的点）为M（2，
），与x轴在原点右侧的第一个交点为N（6，0）．求这个函数的解析式．这个函数的图象怎样变换就得到函数
的图象？
（18）（本小题满分12分）
某单位6个员工借助互联网开展工作，每个员工上网的概率都是0.5（相互独立）．
⑴ 求至少3人同时上网的概率；
⑵ 至少几人同时上网的概率小于0.3？
（19）（本小题满分12分）
设A、B为球面上两点，它们分别在北纬60º和30º的纬线圈上，且经度差为90º，设地球半径为R，求A、B两点的球面距离．
（20）（本小题满分12分）
已知：m、n是平面内的两条相交直线，直线l与的交点为B，且
，
．
求证：
．
（21）（本小题满分12分）
讨论直线
与双曲线
的公共点个数．
（22）（本小题满分14分）
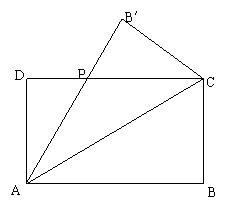设矩形ABCD（AB>CD）的周长为24，把它关于AC折起来，AB折过去后交DC于P．设AB = x．求△ADP的最大面积及相应的x值．